몽키로 전력 변환하기

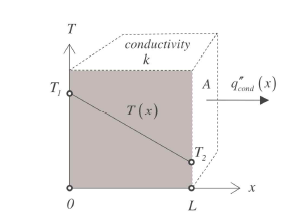
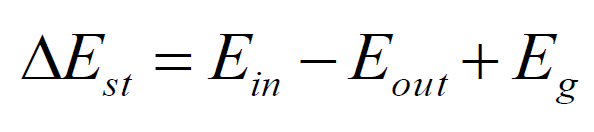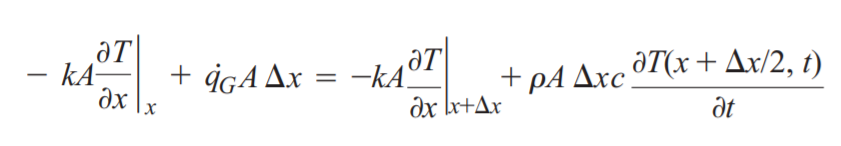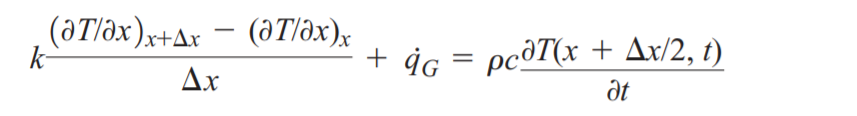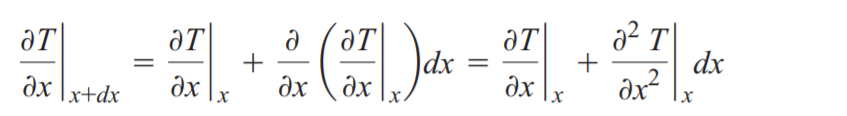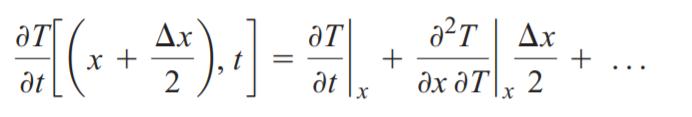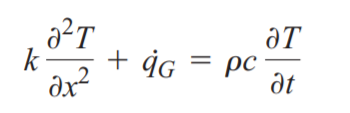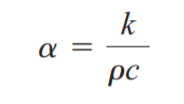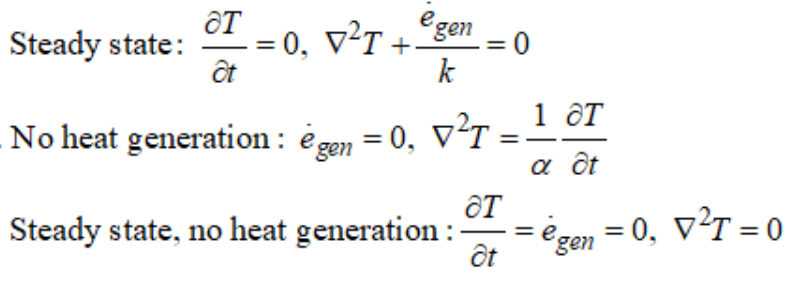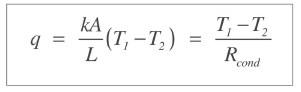이전 포스팅에서의 열생성이 없는 정상상태의 1차원 열전도식의 결론에서 열저항의 개념이 들어가게 되는데

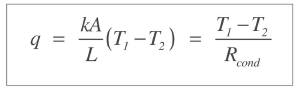
이 식에서 R=L/KA이고

이러한 열저항 system을 이용하는 이유는 계산의 양을 줄이기 위함입니다.

아래의 상황에서 열저항은 우리가 옴의 법칙 처럼 사용하여 열전달율(Heat transfer rate)를 구할 수 있습니다.

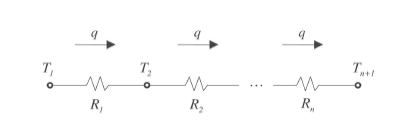
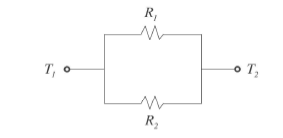
직렬 = R_tot = R1+R2+R3+......

병렬 = R_tot = (R1^-1 + R2^-1 + R3^-1......)^-1

이러한 열저항을 사용하면 아래와 같이 다른 물성치를 가진 복합벽의 경우에서 용이하게 사용될 수 있습니다.

.

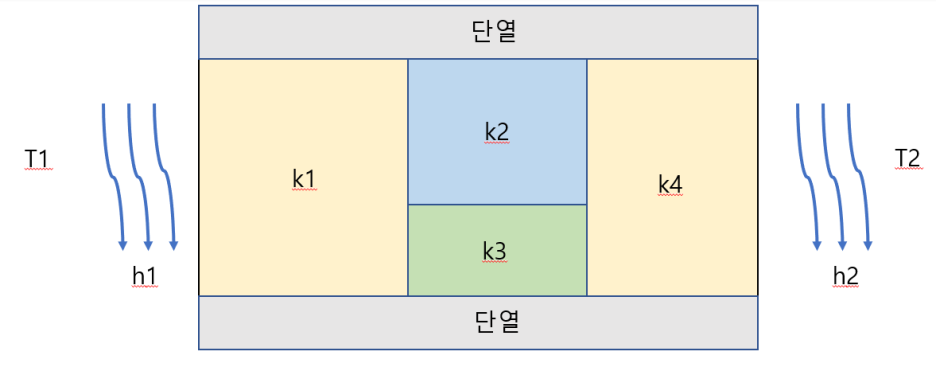
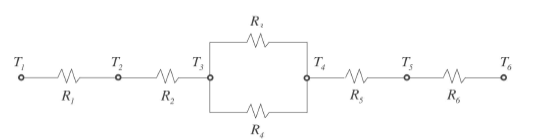
여기서 중요한 점은 열전달율 q[w]는 변하지 않는다는 점입니다.

왜냐하면 에너지는 보존되기 때문에 각지점에 따라 k값에 의해 온도는 달라질 수 있으나

steady state이기 때문에 시간은 고려되지 않아 열전도율은 변하지 않고 일정하게 유지됩니다.

이러한 조건을 이용하여 문제를 많이 풀기 때문에 알아두시는 것이 좋습니다.

위의 열저항시스템을 통해 열전도율 q[w]를 구하는 법은 직렬과 병렬의 전체 열저항을 계산한 후 양끝의 온도 T1,T6만을 이용하여 q를 구할 수 있습니다

이러한 방식은 건축에서 단열을 위해 많이 계산하고 꽤 정확한 결과를 얻을 수 있습니다.

아래의 표는 지금까지 유도방식을 바탕으로 cylinderical coordinate spherical coordinate의 좌표계로 계산했을 때의 결과값을 나타내고 있습니다

h는 대류열전달계수로 다음포스팅에서 다루도록 하겠습니다

C.V을 잡고 에너지보존을 적용하고

k = 열전도율[w/m*k]

q = heat transfer[w]

c = 비열

열전달 에너지보존식에서는 열에너지만 고려합니다.

1차원 열전도 방정식이기에 전미분에서 x성분만 이용하였고 y와z의 길이는 단위길이로 하면 다음과 같은 식이

도출됩니다. 아래식에서 2차미분이 나오는 이유는 미소길이 x의 이동에 따른 온도변화를 미분한 것이기 때문에 2차미분이 적용된 것입니다.

단위가 -인 이유는 열의 이동은 감소하는 방향으로 진행하기 때문입니다.

푸리에 법칙에서 2차미분부터는 매우작아지기 때문에 무시하게 되면 다음과 같은 식으로 정리됩니다.

최종식은 아래와 같이 나오게 됩니다

열확산계수는 다음과 같이 정의됩니다.

이 두 상태의 조건이 적용되면 1차원 열생성이 없는 정상상태의 열전도 방정식은 아래와 같이 나옵니다

(steady state no heat generation 1D conduction equation)

여기서 R_cond는 열저항 개념이 적용되는 것인데 다음 포스팅에서 다루도록 하겠습니다.