몽키로 전력 변환하기

만약 stream function이 일정한 경우를 생각해보면 다음과 같이 표현됩니다.

위의 최종식을 보면 stream line(유선)의 식과 같은 것을 확인할 수 있습니다.

이것을 통해 stream function이 일정하다면 유선과 같고 이름에 왜 stream이 붙었는지를 알 수 있습니다.

streamline에 관한 내용은 streamline 포스팅 참조

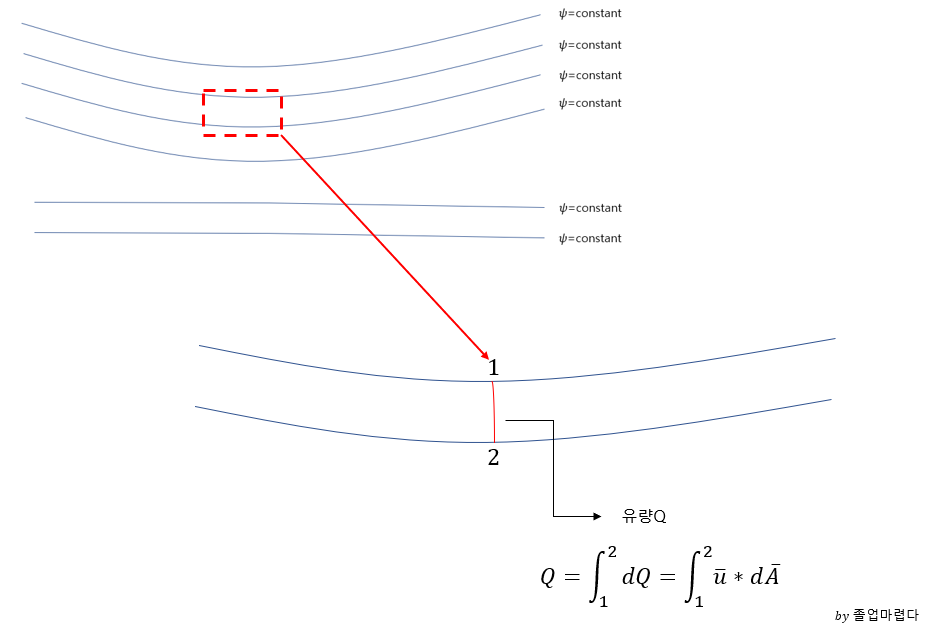
stream function이 일정하다면 일정한 stream line사이의 유량을 구해보면 다음과 같습니다.

즉 일정한 stream function을 안다면 streamline의 차를 통해 유량의 변화를 알 수있습니다.

다음으로는 irrotational flow에서의 vorticity에 대해 알아보도록 하겠습니다.

즉 stream function이 irrotational flow이라면 laplace equation을 만족하여

앞선포스팅에서 확인했듯이 continuity equation을 만족하기 때문에 물리적으로 타당하다 할 수 있습니다.

다음으로는 velocity potential과 stream function의 관계에 대해 알아보도록 하겠습니다.

위와 같은 결과를 그림으로 표현하면 아래와 같습니다.

laplace equation을 통해 velocity potential을 얻고 위와 같은 velocity potential과 streamline(constant stream function)의 관계를 통해 flow pattern을 알 수 있습니다.

쉽게 말하면

속도

potential flow에서 laplace equation을 취하고 gradient로 속도를 구할 수 있습니다.

압력

베르누이방정식을 통해 pressure을 구한다.

(베르누이방정식은 streamline상에서만 유효합니다)

(베르누이방정식 포스팅 참조)

즉 Potential flow을 이용하면 비선형인 Euler equation을 풀지 않고서도 속도와 압력을 알 수 있습니다.

유체의 유동을 표현하는 방법은 총 3가지로 Pathline streakline streamline에 대해 알아보도록 하겠습니다.

Pathline(유적선)

pathline은 Lagrange한 방법으로 유체입자를 표현한 것으로 유체입자를 일정시간동안 궤적을 그린것으로

다음과 같습니다.

streakline(유맥선)

streakline은 주어진 시간동안에 유체입자가 유선을 따라 진행항 경로로

어떠한 지점을 정해놓고 그 지점을 지나는 입자들의 이동을 이은 선입니다.

strickline의 특징으로는 streakline선상에 있는 유체입자라면 이전시간에 특정한 지점을 지난 유체들입니다.

이 streamline을 보면 streamline을 안다면 속도장을 알 수 있다라고 볼 수 있습니다

potential flow란?

irrotational ,inv

icid flow 에서 속도와 압력을 알수있는 방법중 하나입니다.

potential flow는 invicid 영역이기 때문에 처음에 rotation하는 유체의 경우에는 계속해서 rotation하고 irrotation하는 유체는 계속 iroration합니다.

potential flow를 사용하면 continuity equation과 Euler equation을 풀지 않고 속도장을 알 수 있는 방법으로

이전포스팅에서 경계층영역이 viscous flow영역이므로 경계층 밖의 속도와 압력을 구하고자 할 때 이용됩니다.

이러한 potential flow를 굳이 사용하는 이유는

Euler equation이 비선형이기에 못 풀어서 사용합니다.

potential flow를 시작하기 전에 potential flow에서 사용되는 기본수식에 대해 알아보도록 하겠습니다.

유체입자유동 기본수식

potential flow에서 나오는 gradient divergent curl의 정리입니다

gradient :▽P

스칼라함수의 미분으로 각 좌표로 미분한 후 단위vector의 곱을 더한 것으로

3차원에서의 각각의 미분이라고 보면 됩니다.

divergent :▽· P

내적의 형태로 나타내고 ▽· P 와 같이 표현됩니다.

내적을 취하였기 때문에 방향성을 상실하고 크기만을 나타내는 스칼라함수가 됩니다.

curl :▽x P

외적의 형태로 나타나고 ▽x P와 같이 표현됩니다.

이는 유체의 한 입자가 회전한 정도를 나타내는 것입니다.

여기서 중요한 사실은

divergent 와 curl ,curl과 divergent를 취하게 되면 수학적으로 모두 0이됩니다.

kelvin helmholtz theorem

아래와 같은 유동이 있을경우를 생각해 보도록 하겠습니다.

1.only normal force

2.irrotational

이러한 조건을 가진 것이 potential flow 또는 ideal flow라고 합니다.

이것이 kelvin helmholtz theorem 입니다.

이러한 potential flow를 이해하기 먼저

유체입자의 유동은 중요한 것이 vortex와 circulation이 있습니다.

vortex는 유체하나의 입자가 회전하는 세기를 나타내는 것이고 circulation은 단면을 지나가고 있는 유체입자의

회전세기의 총 합입니다.

Velocity potential

Euler equation을 보면

결론적으로 Euler equation을 만족하는 해중 하나는 vortex가 0일 경우 즉 irrotation일 경우 만족합니다.

다음으로 알아볼 것은 velocity potential입니다.

이러한 velocity potential은 euler equation을 만족하므로

물리적으로 타당하기 위해 이젠 continuity equation을 만족하는지 보아야 합니다.

continuity equation은 다음과 같았음을 저번 연속방정식 포스팅에서 확인해 본 바 있습니다.

여기서 incompressive를 만족하기 위해 다음과 같아야 합니다.

앞에서 euler equation을 통해 momentum conservation을 만족하였고

continuity equation을 통해 mass conservation을 만족하면되는데

여기서 의미하는 것은

laplace equation을 만족하는 모든 해는 velocity potential이 될 수 있다는 것입니다.

각 좌표계에 따른 laplace equation은 다음과 같습니다.

지금 까지로 보면 laplace equation을 만족하는 해 즉velocity potential은 irrotational incompressive invicid flow하에 있고 velocity potential에 gradient를 취하게되면 속도를 알 수 있습니다.