몽키로 전력 변환하기

 

수평관의 C.V을 통해 식을 도출하기전에 먼저 pipe내의 유동에 대해 먼저 알아보도록 하겠습니다.

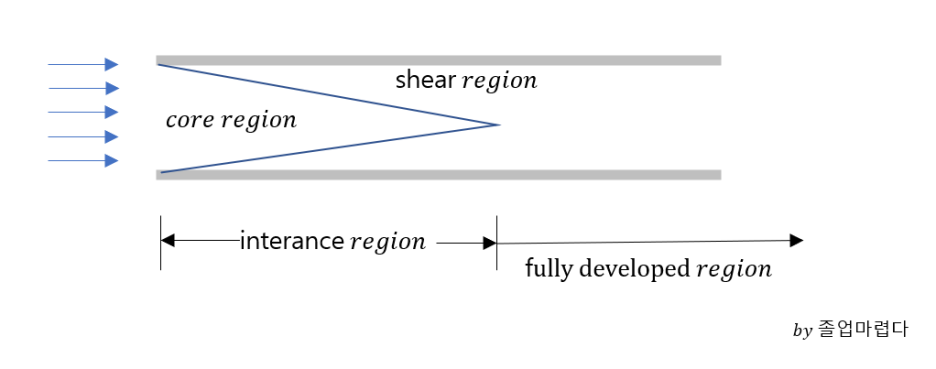
pipe내에 유체가 들어오면 입구구역(interance region)과 완전발달구역(fully developed region)으로 나뉘게 됩니다. fully deveoped flow구역은 x방향으로 진행되어도 속도의 변화가 더이상 일어나지 않는 것으로

Navier stokes equation의 momentum을 통해서도 알 수 있습니다.

비압축성 pipe에서의 Navier stokes equation에서 momentum은 좌표축이 3개 (r,x,θ)로 다음과 같이 표현됩니다.

 

위의 결과는 pressure는 x만의 함수라는 점을 알 수 있고 이를 통해 1개의 변수만을 가지는 상미분 으로 풀이 될 수 있다는 것을 알 수 있습니다.

위의 미분방정식을 풀기위해서는 다음과 같은 boundary condition이 적용됩니다.

1.r=r_0 일 때 속도 u가 0인 noslip condition

2.r=0일때 속도u는 최대속도 u_max

결론적으로 x에따른 속도분포는 다음과 같은 결과로 나오게 됩니다.

 

 

 

이렇게 Navier stokes equation를 이용해 푸는 방법이 있고

C.V을 잡고 풀수도 있는데 다음과 같이 유도됩니다.

 

pipe내부의 유동은 fully developed flow에서 pressure는 x의 함수이고 가속도는 0이라는 것을 조건으로 이제 pipe에 C.V을 잡고 풀이를 진행하도록 하겠습니다.

 

 

다음과 같은 수평원관에서의 전단응력에 대해 식과 속도분포를 유도해 보도록 하겠습니다.

Reynolds transport theorem에서의 운동량보존식을 이용하면 다음과 같습니다.

유체역학에서 유체에 작용하는 힘은 다음과 같습니다.

1.표면력(수직, 전단)

2.체적력(중력)

여기서는 수평관이기에 중력의 영향은 무시하고 표면력만 구하도록 하겠습니다.

레이놀즈수송정리에 관한내용은 레이놀스 주송정리포스팅을 참조하시기 바랍니다.

 

이러한 문제들은 다음과 같은 조건하에 유도됩니다.

1.horizontal pipe

2.incompressive flow

3.fully developed flow

4.steady state

5.axisymmetry(중심축기준 각변화에 따라변하지 않는다)

Reynolds transport theorem of momentum conservation

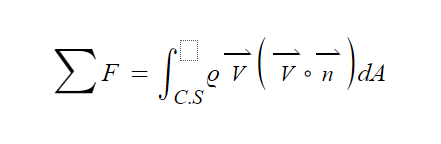
최외각 전단응력 즉 r=R일 때 전단응력은 다음과 같이 유도됩니다.

 

 

 

결론은 다음과 같은 전단응력과 이에 따라 포물선의 유동속도를 보이게 됩니다.

 

가속도가 0인 이유는 pressure force와 viscous force가 상쇄되기 때문에 가속도가 0입니다.

여기서 전단응력은 뉴턴유체(linear)이기에 전단응력분포는 다음과 같이나옵니다.

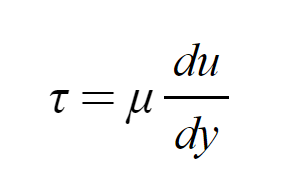
속도분포에 관한식은 층류 뉴턴유체일때의 전단응력인 위의 식에서부터 시작됩니다.

 

 

 

위 식에서 du가 0이되는 이유는 fully developed이기 때문입니다.

속도분포를 보면 2차를 보이고 있기 때문에 포물선형태를 보이고있음을 알 수 있습니다.

 

이 solution이 Poiseuille flow solution 입니다

 

다음으로는 유량관계식에 대해 알아보도록 하겠습니다.

체적유량은 면적에 유동속도를 곱하는 것인데 위에서 구한 속도분포를 통해 아래의 유량을 구하고

 

최종적으로 나온식이 유명한 하겐-포아죄유식(hagen poiseuille's law)입니다.

 

 

 

원관에서의 poiseuille flow 가 hagen poiseuill's flow입니다.

여기서 중요한 점은 fully developed라 가정하고 나온 식이기에 pipe의 입구에서 적용할 수 없습니다!

 

이제 마지막으로 벽면에 작용하는 wall shear stress에 대해 알아보도록 하겠습니다.

 

 

위 wall shear stress를 통해 유추할 수 있는점은 유량을 늘리기 위해 유속을 증가시킨다면 wall shear stress도 커지기 때문에 이를 버틸 수 있는 배관인지를 먼저 생각하고 설계해야 할 것입니다.

저도 공부하는 중이지만 설계라는 것이 고려해야 할 것이 많고 요소 하나의 실수로도 큰 사고가 발생할 수 있으므로

책임감을 가지고 엔지니어가 되기위해 더욱 많은 노력이 필요하다고 생각합니다.

 

지금까지 수평관에서의 속도 전단응력 유량(하겐-포아죄유식)과 wall shear stress에 대해 알아보았습니다.

 

 

오늘은 유체역학에서 중요한 방정식중 하나인 베르누이방정식에 대해 알아보도록 하겠습니다

베르누이방정식은 유선상에서의 정압과 동압의 합은 항상 일정하다라는 식입니다

아래와 같이 C.V을 잡고 아래 두개의 가정하에 적용이 됩니다.

1.frictionless flow (즉 마찰은0)

2.along streamline in frictionless flow

먼저 Reynolds Transport thorem (레이놀즈 수송정리)를 바탕으로

mass conservation과 momentum conservation을 정의하게 됩니다

레이놀즈수송정리에 관한 유도과정은 레이놀즈수송정리 포스팅을 참조하시기 바랍니다

​

 

1. mass conservation의 적용 ( B=1, β =1)

2. The linear momentum conservation(B=mv, β =v) 

 

 

 

여기서 differential이 round로 변한이유는 아직 steady state인지 incompressive인지 결정되지 않아 round로

쓴 것으로 시간에 따라 변할 수 있는 상태입니다.

 

유체역학에서 유체에 작용하는 힘 F는 3가지가 있습니다

1.gravity(중력)

2. pressure

3.shear force (frictionless flow라 가정하였기 때문)

 

이러한 힘들을 위의 식에 대입하면 다음과 같이 도출됩니다

 

위의 결과에서 steady incompressive flow의 경우 최종적으로 다음과 같은 베르누이 방정식이 도출됩니다.

 

 

베르누이방정식의 의미는 유선상에서의 정압과 동압의 합은 항상일정하다를 나타냅니다.

유체가 흐르다 수평의 평판과 만나게 되면 평판의 점성에의한 마찰로 흐르던 속도가 줄게되고 이에따라 다음과 같은 속도 profile을 갖게 됩니다.

여기서 점성의 영향을 받는 viscous layer인 boundary layer와 점성의 영향을 받지 않는 booundary layer 밖의 영역으로 나뉘게 됩니다.

 

figure (1) 좌 boundary layer 우 velocity profile

여기서 viscous의 영향을 받는 경계층 두께의 기준은 원래유동속도 U_inf의 99%(책마다 조금씩 다릅니다)가

되는 지점으로 정의합니다.

유체역학에서는 유체의 거동(위치 속도 압력)을 알기가 어려운점이 있기때문에 대부분의 식들은 실험을 통해 나온결과가 많습니다.

실험에 사용되는 모형 이외에도 같은식을 사용하기 위해 무차원화 된 단위를 사용합니다.

아래의 그림을 보면 boundary layer에서 속도는 x에따라 변하게 되는데 물리량을 무차원화 하면 하나의 그래프로

오늘은 여러가정하에 유도하여 적용할 수있는 B.L에 적용되는 식에대해 알아보도록 하겠습니다

표현이 가능하다는 것을 표현한 그림입니다.

이때 속도u 는 아래(1) 와 같이표현이 가능하다 가정하고 이를 Similarity solution이라고 합니다.

블라시우스상사

 

이렇게 가정하였을 때 continuity equation(질량보존)과 Navier-Stokes Equation운동량보존을 만족하면

무차원화한 것이 유효하다고 볼 수 있습니다.

이러한 무차원화에 대한 증명을 하기 전에 B.L(Boundary layer)에 대한 명칭과 의미에대해 알아보도록 하겠습니다.

 

이러한 블라시우스 상사가 성립되면 좋은점은

유체가 받는 stress와 음직임은 속도 V와 pressure만 알면 Navier-stokes, continuity equation을 사용하지 않고도 유체의 거동을 알 수 있다는 점입니다.

 

경계층이론

 

 

위의 3개의 boundary layer에서의 명칭에대한 의미와 유도를 하기전에 폰카르마적분방정식 먼저 알아보도록 하겠습니다.

 

 

 

폰카르만 적분방정식

 

C.V을 잡고 폰카르만 적분방정식을 통해 층류와 난류 모두의 속도분표를 알 수 있는데 만약 속도분포를 안다면

연속방정식(질량보존)과 운동량보존(나비에스토크스)를 통해 경계층두께 벽전단력 그리고 항력을 구할 수 있습니다.

먼저 폰카르만 적분방정식에 대해 유도하면

 

 

(1)Mass flux

 

 

(2) Forces

 

 

 

(3) momentum flux

 

 

 

1.boundary layer thickness

 

boundary layer는 경계층두께로 정의되고 초기유동속도의 99%의 위치까지의 높이를 의미합니다

이러한 경계층두께는 난류가 층류에 비해 빠르게 U_99에 접근하는 것을 볼 수 있습니다

그렇기 때문에 난류가 층류에 비해 경계층 두께가 얇은 특징이 있습니다.

 

2.displacement thickness

위의 폰카르만 적분방정식에서 (1) mass flux를 보면

U_inf*H의 체적유량으로 들어오던 초기유량이 평판의 점성에 의해서 속도가 줄게되고 이에 따라

질량보존을 만족하기 위해 증가한 경계층두께를 나타내는 것 입니다.

 

 

 

3. momentum thickness

momentum이 평판의 수직으로 확산되면서 확장되는 두께를 나타내고 운동량감소를 나타냅니다.

 

 

drag는 마찰에의한 항력으로 아래와 같습니다.

since

위와 같은 조건에 의해 다음과 같이 drag가 도출됩니다.

결론적으로 momnetum감소에 따른 Drag는 다음과 같이 도출됩니다.

 

지금까지 점성에 의해 발생하는 Boundary layer상에

displacement thickness ,momentum thickness 과 이로인한 Drag force의 유도과정에 대해 알아보았습니다.

 

골프공을 자세히 보신적이 있나요?

골프공을 보면 움푹파인 홈들이 있는데 이를 딤플이라고 합니다.

이러한 딤플에 의해 골프공이 멀리 나가게 되는데,

오늘은 왜 골프공이 딤플에 의해 멀리나아가게 되는지 유체역학의 원리를 적용하여 설명하도록 하겠습니다.

결론먼저 쓰면

- 딤플은 유체의 흐름을 난류로 만든다.

- 난류에 의해 박리점이 공 뒤로 간다.

- 이로인해 형상항력을 줄일 수 있다.

이러한 결론을 내기 위해 몇가지 유체역학의 이론에 대해 설명하면

먼저 유체의 흐름에는 층류와 난류가 있습니다

층류는 층층히 나뉘어져가서 층류고, 난류는 규칙없이 난잡하게 유동합니다.

이러한 층류와 난류를 정의하는 무차원의 수를 레이놀즈수(Reynolds number)라고 합니다

각각의 레이놀즈수는

층류 Re < 2300

난류 Re > 4000

입니다

층류와 난류형태로 흐르는 유체가 고체를 만나면 고체의 벽면을 따라 경계층(boundary layer)을 형성하고

점성효과(viscous)를 받는 경계층 내부구역과 점성효과를 안받는 경계층 외부구역(inviscous)으로 나뉩니다

이러한 경계층의 기준은 초기유동속도의 99프로가 되는 곳으로 아래 유동프로파일(유동속도)그래프를 보면 난류가 층류보다 가파르게 속도가 증가함을 볼 수 있습니다

즉 표면에서 수직방향으로 올라갈 때 난류가

초기 유동속도의 99프로에 더 빠르게 근접하므로 경계층 영역의 길이가 짧게 형성됩니다.

경계층의 두께의 경우는 난류가 층류이후에 발생함으로 난류가 더 두껍게 나타납니다.

경계층 두께 는

층류 < 난류 가 됨을 알 수 있습니다.

경계층의 영향을 받는 길이는

층류>난류

다음으로 알아야 할 이론은 박리입니다.

박리란 유체가 고체면을 만났을 때 점성효과로 인해 속도가 줄어 고체의 속도를 따라가지 못해 떨어져 나가는 현상입니다.

박리의 특징은 순압력구배(dp/dx < 0) 에서 역압력구배(dp/dx > 0)로 넘어가는 지점으로 가장 압력이 낮은 지점입니다.

위 사진과 같이 난류일경우 박리점이 뒤에 있음을 볼 수 있습니다.

난류이면 왜 박리점이 뒤로 가는가?

여기서 Re 수와 C_D의 관계를 나타낸 그래프가 아래에 있습니다.

위 그래프를 보면

난류가 층류보다 C_D값이 낮기 때문에 Drag force를 적게 받는다는 것을 알 수 있습니다.

정리하면

경계층의 길이 층류 >난류 로 난류가 viscous영향을 적게 받고 C_D 값이 낮기 때문에 난류의 박리가늦게 발생합니다 .

이러한 낮은압력의 박리점이 뒤로감으로서 압력차에 의한 형상항력을 받는 공의 면적이 줄어 더 멀리 나갈 수 있는 것 입니다.

결론

- 딤플은 유체의 흐름을 난류로 만든다.

- 난류에 의해 박리점이 공 뒤로 간다.

- 이로인해 형상항력을 줄일 수 있다.

이로인해 딤플이 있는 골프공이 멀리나가게 됩니다