
오늘은 이러한 potential flow를 시작하기 전에 압력과 점성에의한 유체입자 유동에 대해 알아보도록 하겠습니다.
만약 아래와 같은 상황
조건 1.fully developed flow
2.steady state
3. constant pressure gradient
일때 한쪽 평판이 u_w만큼 이동할때
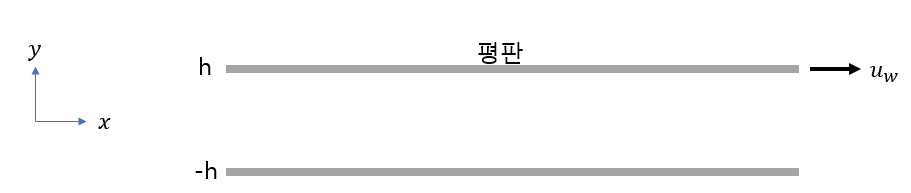
위의 상황을 보면
poise flow는 pressure와 전단응력이 상쇄도고
couette flow는 두 평판사이의 반대되는 전단응력에 상쇄되어 가속도는 0이 됩니다.
그렇기 때문에 다음과 같은 continuity equation과 Navier-stokes momentum equation이 도출됩니다.
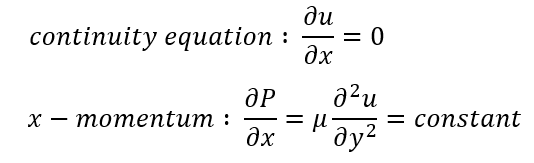
위의 식에서 속도를 구하기 위해 boundary condition을 아래와 같이 사용합니다

이러한 B.C을 통해 적분하고 대표속도인 u_w로 무차원화 하면 다음과 같은 결과를 얻을 수 있습니다.
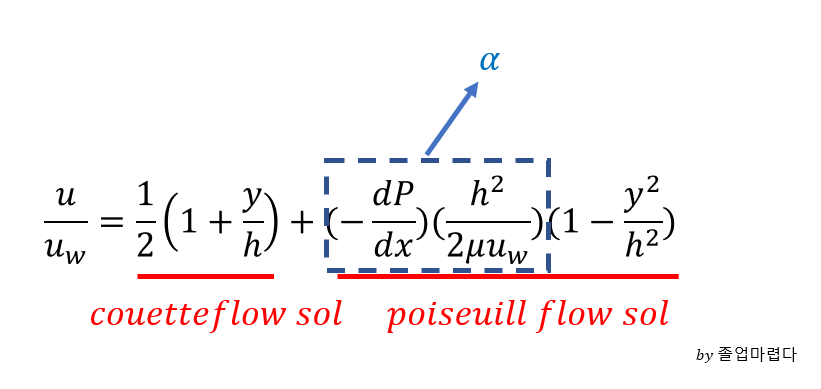
위 solution을 보면 couette flow solution과 poiseuill flow sol의 합으로 나와있는데
이러한 중첩(super position)이 가능한 이유는 위에서 가속도가 0이되어 Navier-stokes에서 비선형인 부분이 사라졌기 때문입니다.
poise flow sol에서 박스부분을 알파라 하고 알파의 변화에 따라 다음 그림과 같은 속도분포를 가지게 됩니다.
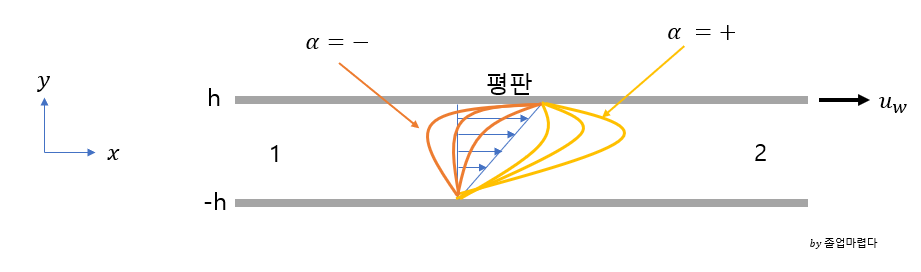
그림을 보면 아래평판은 no slip sol이기 때문에 속도는 0이고
1.압력변화가 0 즉 dp/dx = 0
파란색처럼 속도분포가 되고 이는 couette flow 와 같음을 알 수 있습니다.
2.압력변화가 음수 dp/dx = -
2의 압력이 1보다 작을 경우 알파가+인 노란색 속도분포가 나타납니다.
3.압력변화가 양수 dp/dx = +
2의 압력이 1보다 큰 경우로 알파가 -인 주황색 속도분포로 역방향 속도분포가 발생할 수 있습니다.
(여기서 알파가 -0.25일 경우에는 wall shear stress가 0이되고 박리가 발생합니다.)
(알파가 -0.25보다 더 작아질 경우에는 역류 back flow가 발생합니다.)
다음으로는 평판이 움직이지 않는 경우
즉 u_w가 0인 경우에 대해 알아보도록 하겠습니다.
그럼 위의 식의 solution이 poiseuille flow solution만 남게 됩니다.
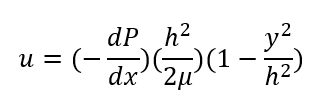
이때 최고속도는 y=0일 경우이고 체적유량은 Au를 적분한 것으로 다음과 같이 나오게 됩니다.
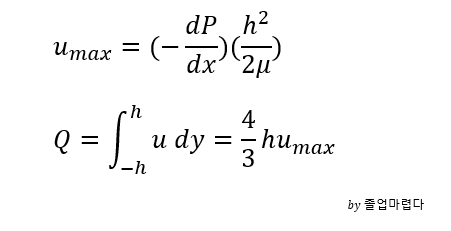
위의 Q를 보면 평판이라 하겐포아죄유식과는 다른 것을 확인 할 수 있습니다.
그리고 아래는 평균속도와 벽면의 전단 drag coefficient 입니다.
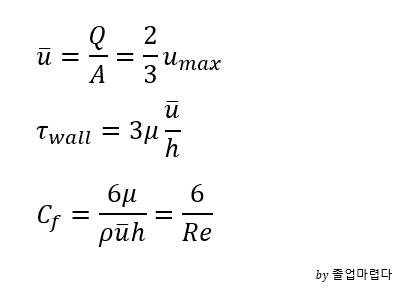
지금까지 pressure gradient에 의한 유체유동 viscous에 의한 유체유동에 대해 알아보았습니다.
'기계공학(Mechanical Engineering) > 유체역학(Fluid Mecahnics)' 카테고리의 다른 글
| 유체역학 입자유동 회전 와도 순환(rotation,vorticity,circulation) (0) | 2022.10.21 |
|---|---|
| 관 마찰계수 (수두손실) 유도 (0) | 2022.10.21 |
| 수평pipe에서의 층류유동hagen poiseuille's law의 유도 Navier-stokes and C.V sol (0) | 2022.10.21 |
| Bernuii Equation 유도(베르누이방정식) (0) | 2022.10.21 |
| 경계층이론 boundary layer(feat 블라시우스상사,폰카르만 적분방정식) (0) | 2022.10.21 |