몽키로 전력 변환하기

그 중 C.V내에서의 질량보존을 나타내는 continuity equation에 대해 알아보도록 하겠습니다.

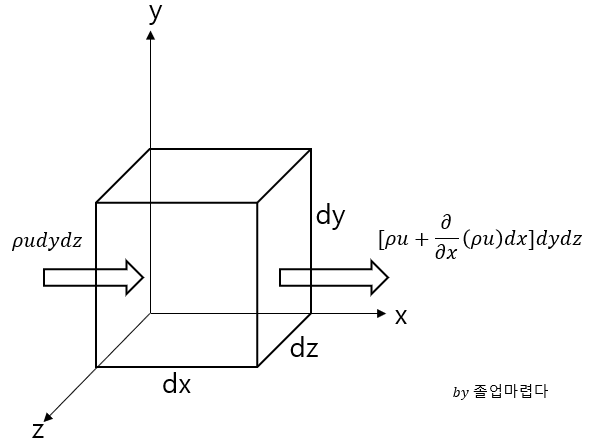
위와 같은 C.V을 잡고 x방향으로 유체가 흐를 때 아래의 레이놀즈수송정리를 이용하여 다음과 같이 정리됩니다.

steady state에 incompressive flow이므로 C.V의 바깥면인 control surface에서만 유체의 이동을 살펴보면 되고 최종적으로 1번식으로 나오게 됩니다.

1 식을 x y z성분으로 보면 다음과 같이 정리됩니다.

최종적으로 mass conservation을 나타내는 연속방정식(continuity equation)은 다음과 같이 유도됩니다.

다음포스팅에서는 invicid영역에서의 momentum conservation을 나타내는 Euler equation을 알아보도록 하겠습니다.

유체입자의 움직임을 설명하는 유체유동에 대해 알아보도록 하겠습니다.

유체입자의 유동은 다음과 같이 있습니다.

1.Translation

translation은 velocity와 acceleration과 관련이 있습니다.

여기서 중요한 점은 acceleration을 구할 때 전미분을 통해 구해야 한다는 것입니다.

2.volume deformation

3.Rotation and Angular deformation

다음으로는 rotation rate입니다.

위와 같은 rotation rate를 구하기 위해서는 위에서 구한 rotation과 angular deformation의 합으로

구하게 되는데 W의 x,y,z의 합으로 이루어집니다.

또한 앞에 1/2을 없애기 위해 2W를 한것을 vortex라고 합니다.

vortex가 0이면 회전하지 않고 0이 아니라면 회전합니다.

지금까지 유체입자유동의 기본적인 종류에대해 알아보았습니다.

다음과 같은 상태일 때 다음과 같은 C.V을 잡고 force를 계산하면 전단력이 다음과 같이 유도 됩니다.

이후 뉴턴유체이고 베르누이방정식을 적용시키면 다음과 같이 유도됩니다.

위에서 나온 1번식과 2번식을 같다고 놓고 풀면 압력차는 최종적으로 다음과 같이 나옵니다.

위에 h_f가 수두손실입니다.

위의 상황을 보면

poise flow는 pressure와 전단응력이 상쇄도고

couette flow는 두 평판사이의 반대되는 전단응력에 상쇄되어 가속도는 0이 됩니다.

그렇기 때문에 다음과 같은 continuity equation과 Navier-stokes momentum equation이 도출됩니다.