여러 전자장비나 단기통엔진등에는 fin을 통해 발열을 제어하는 것을 실생활에서 흔히 확인할 수 있습니다.
오늘은 이러한 fin을 설계에 적용되는 이론에 대해 알아보도록 하겠습니다.
먼저 fin을 이해하기 위해서는 대학이나 kocw의 무료강의를 통해 열전달강의를 수강하셔야 합니다
이번포스팅에서는 fin을 이해하기 위해 열전달중 전도에 대해 알아보도록 하겠습니다.
전도는 conduction이라하고 고체사이에 입자간의 열전달로 푸리에정리에 따라 유도됩니다.
먼저 유도과정은 다음과 같습니다.
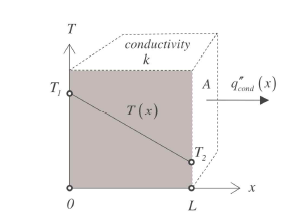
C.V을 잡고 에너지보존을 적용하고
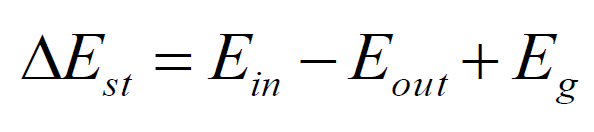
k = 열전도율[w/m*k]
q = heat transfer[w]
c = 비열
열전달 에너지보존식에서는 열에너지만 고려합니다.
1차원 열전도 방정식이기에 전미분에서 x성분만 이용하였고 y와z의 길이는 단위길이로 하면 다음과 같은 식이
도출됩니다. 아래식에서 2차미분이 나오는 이유는 미소길이 x의 이동에 따른 온도변화를 미분한 것이기 때문에 2차미분이 적용된 것입니다.
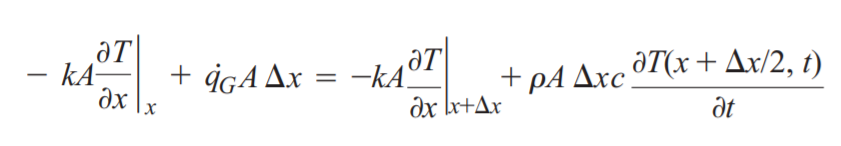
단위가 -인 이유는 열의 이동은 감소하는 방향으로 진행하기 때문입니다.
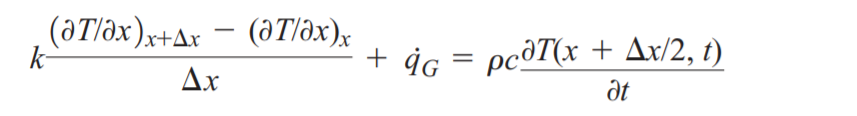
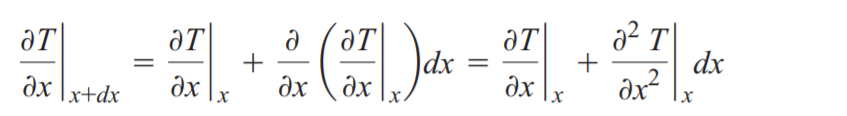
푸리에 법칙에서 2차미분부터는 매우작아지기 때문에 무시하게 되면 다음과 같은 식으로 정리됩니다.
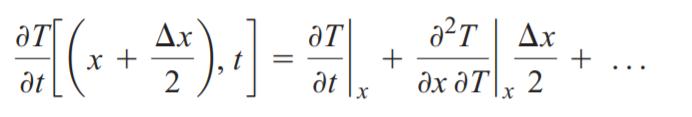
최종식은 아래와 같이 나오게 됩니다
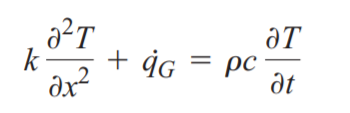
열확산계수는 다음과 같이 정의됩니다.
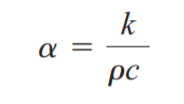
위의 최종식에서 아래와 같은 조건
steady state(시간에 따라 변하지 않는 조건 즉 열전달이 끝난 상태)
No heat generation(내부에서 열생성이 없는 상태)
에 따라 아래와 같이 도출됩니다.
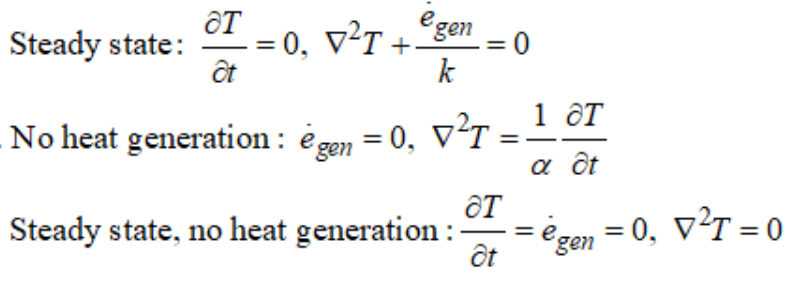
이 두 상태의 조건이 적용되면 1차원 열생성이 없는 정상상태의 열전도 방정식은 아래와 같이 나옵니다
(steady state no heat generation 1D conduction equation)
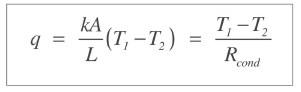
여기서 R_cond는 열저항 개념이 적용되는 것인데 다음 포스팅에서 다루도록 하겠습니다.
'기계공학(Mechanical Engineering) > 열전달(Heat Transfer)' 카테고리의 다른 글
| 핀 열전달 문제 풀이 #14 (0) | 2022.10.29 |
|---|---|
| fin 휜 설계 열전달[Heat transport]#2 열저항(Thermal resistance) (1) | 2022.10.23 |
| 대류열전달 문제해결법 [상사성 similarity] (1) | 2022.10.23 |
| 방정식 수치해법 [엑셀 연립방정식풀이 Gauss seidel feat 열전도방정식] (0) | 2022.10.23 |
| 열전달 계산 Mathlab 프로그래밍(feat.Gauss seidel) (0) | 2022.10.23 |