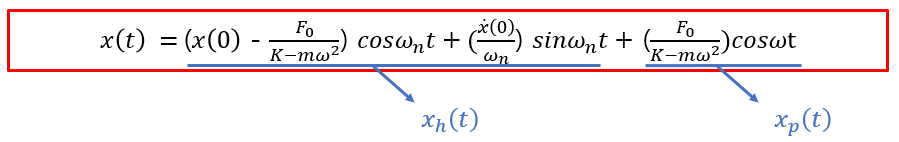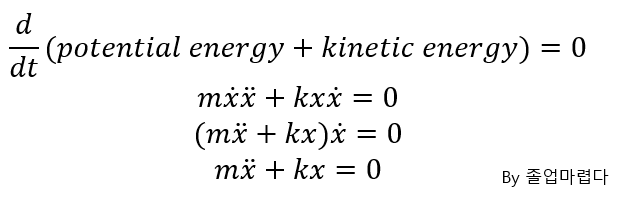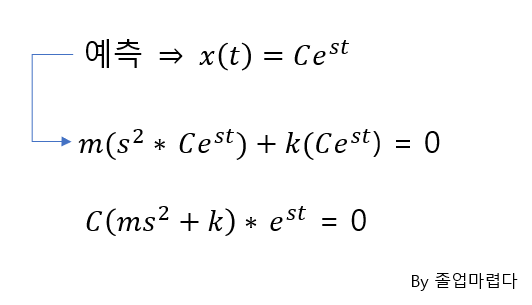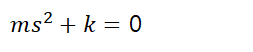몽키로 전력 변환하기

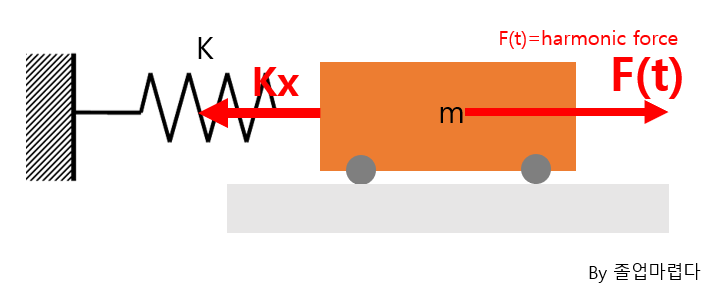
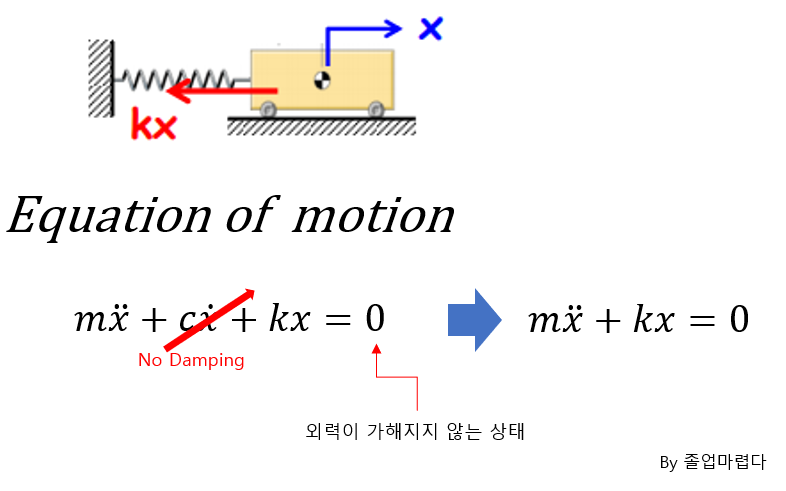
이전에 하던것과 같이 다음과 같은 Equation을 얻을 수 있습니다.

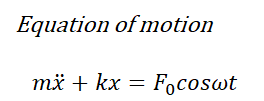
harmonic이란 sin이나 cos이라고 생각하면 됩니다.

이 때 적용되는 방식은 harmonic한 힘이 가진된다면 결과도 harmonic하게 나올 것이다 라고 가정 후 이 예측이 맞는지를 확인하면 됩니다.

우변이 0이 아니므로 자유진동일때와는 다르게 공학수학1때 배운 선형대수학개념을 적용해야 합니다.

결론적으로는 homogeneous solution과 particular solution의 해의 합이 결과가 됩니다.

결론적으로 다음과 같은 결과를 얻을 수 있습니다.

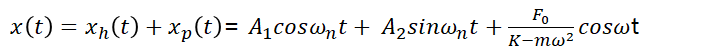
이제 초기조건을 통해 미지수(A1,A2)를 구하고 정리합니다.

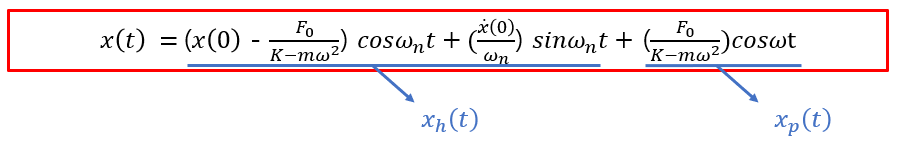
particular solution에서의 amplitude값은 다음과 같이 구할 수 있습니다.

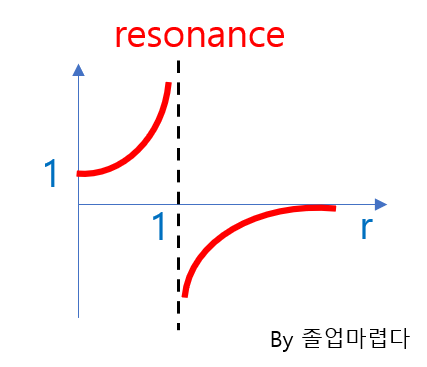
위의 식에서 가진주파수와 고유진동수가 일치하면 공진이 발생한다는 것을 아래의 식을 통해서도 알 수 있습니다.

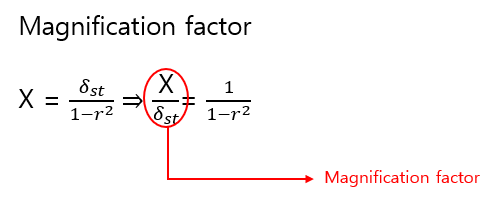
magnification factor의 그래프를 그리면 다음과 같은데 고유진동수와 가진주파수가 일치할 때의 amplitude의 값은 무한이 되는 것을 확인할 수 있습니다.

이전 포스팅에서 고유진동수에 대해 알아보았는데 이번엔 직접 고유진동수를 증명해 보도록 하겠습니다.

아래 조건은 Damping과 가진이 없는 자유진동 상태입니다.

식을 구하는 방법은 Energy conservation에 의해 만들어 집니다.

Solution을 구하는 방식은 위에같이 Newton의 법칙에 의해 식이 만들어지고 이 식의 결과를 먼저 유추한 후 역으로 맞는지를 확인합니다.

x = 진폭, k = 강성, m = 질량 (여기선 질량에 물체의 중심에 점질량으로 몰려있다고 가정합니다.)

아래와 같이 먼저 결과를 예측합니다.