몽키로 전력 변환하기

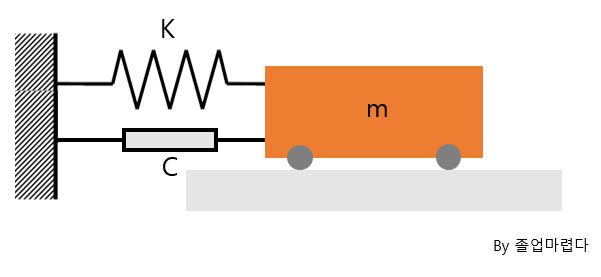
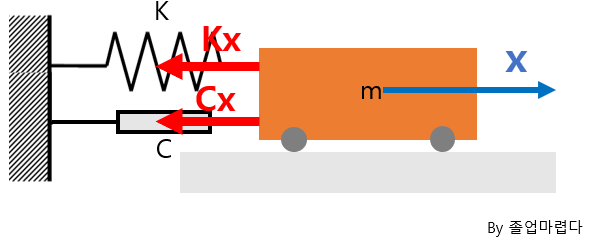
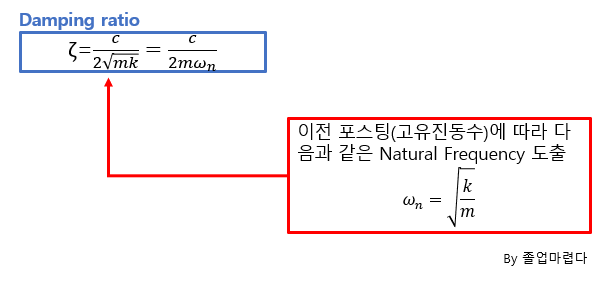
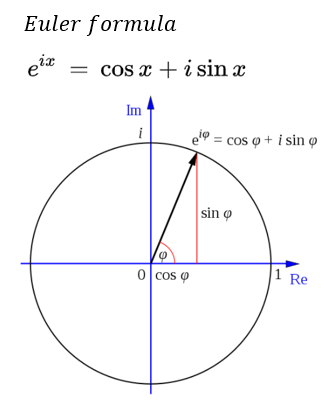
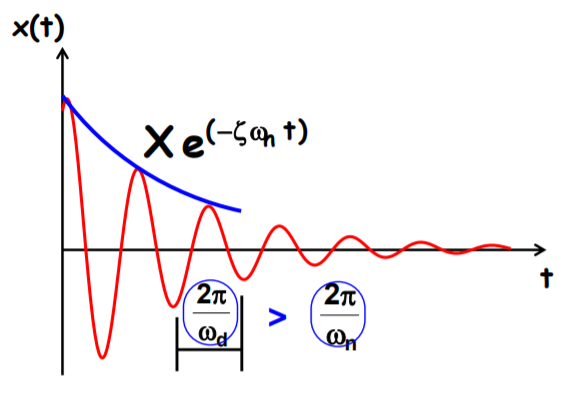
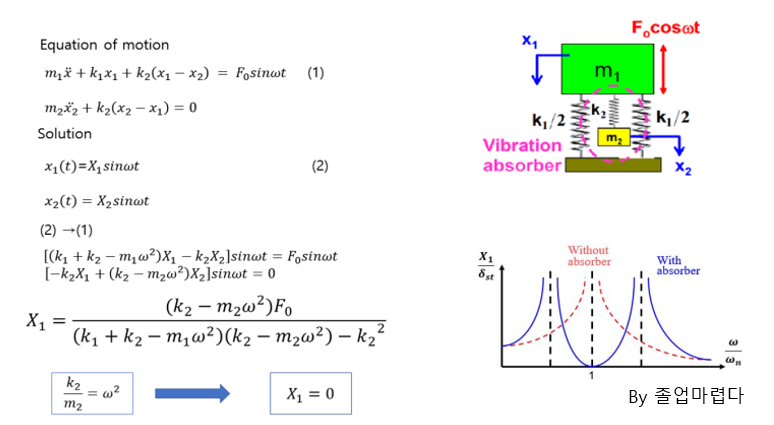
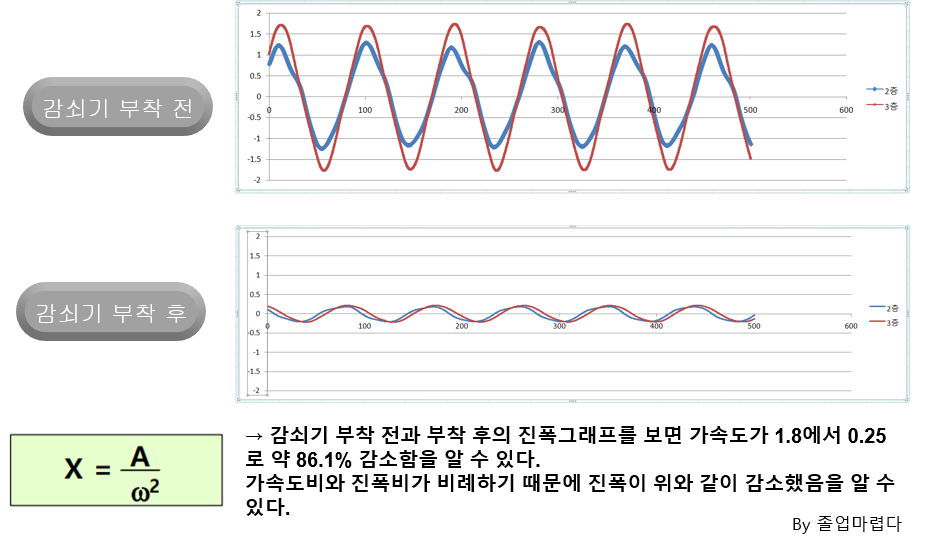
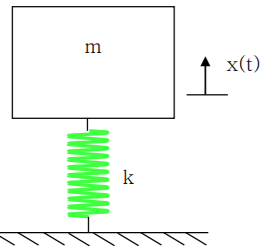
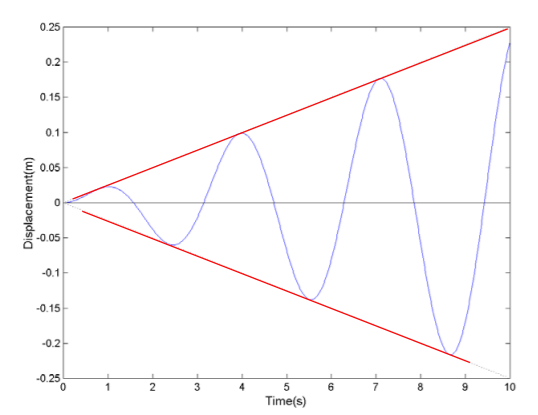
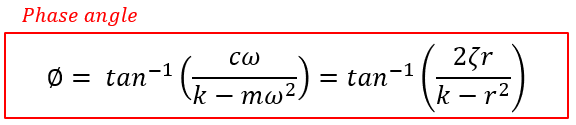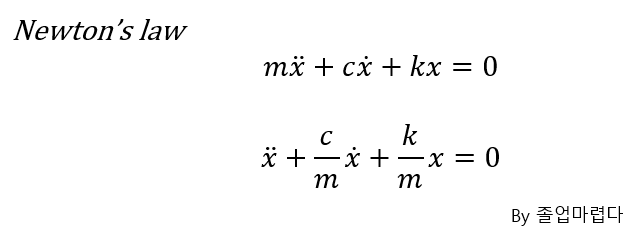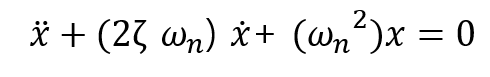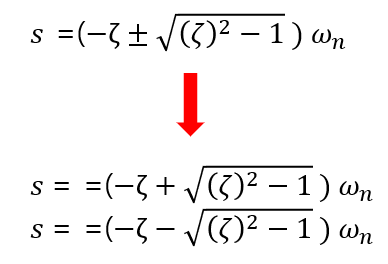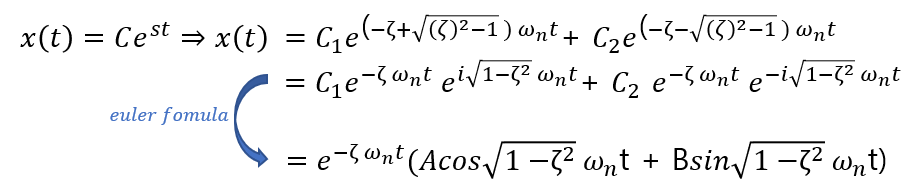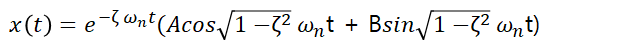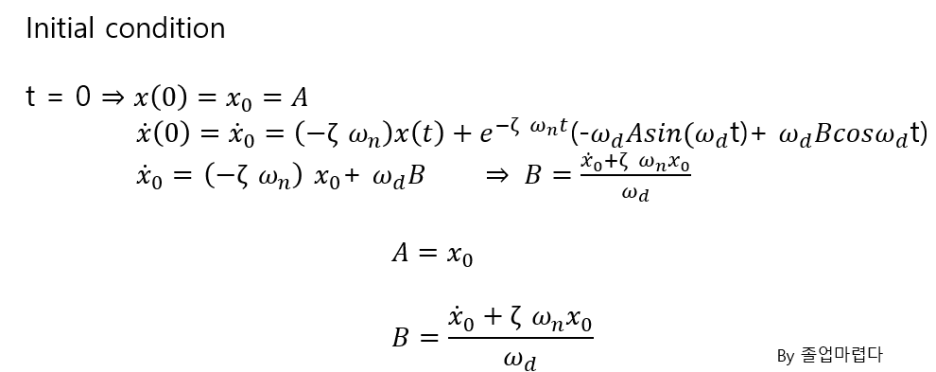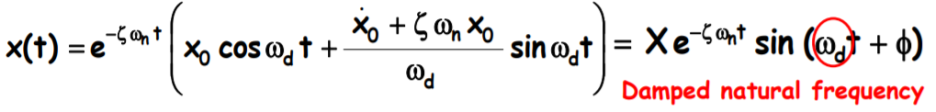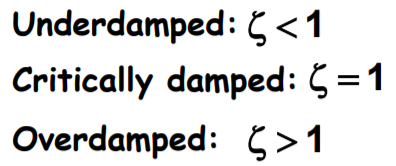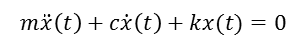감쇠조화가진일경우 진동특성에 대해 알아보도록 하겠습니다.

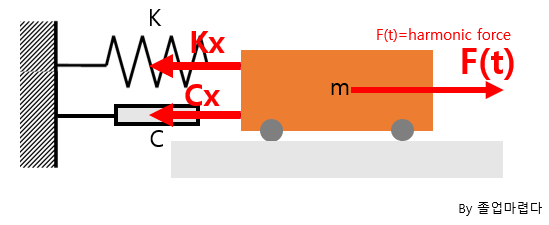
이전에 하던것과 같이 다음과 같은 Equation을 얻을 수 있습니다.

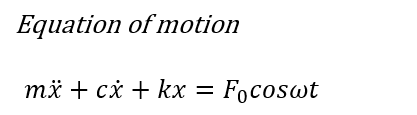
우변이 0이 아니기에 공학수학의 선형대수부분의 풀이방법을 따라야 하고 감쇠자유진동포스팅에서 했던 대로

homogeneous solution과 particular solution을 구해야 하는데 homogeneous solution는

다음과 같은 과정을 통해 나오게 되었습니다.

Homogeneous Solution

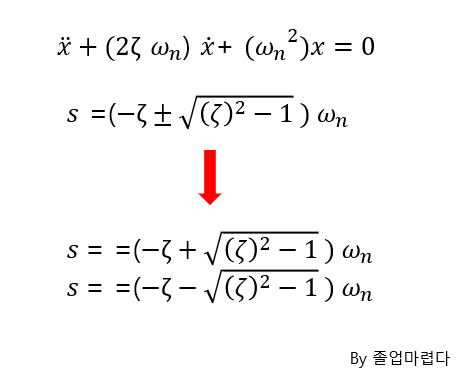
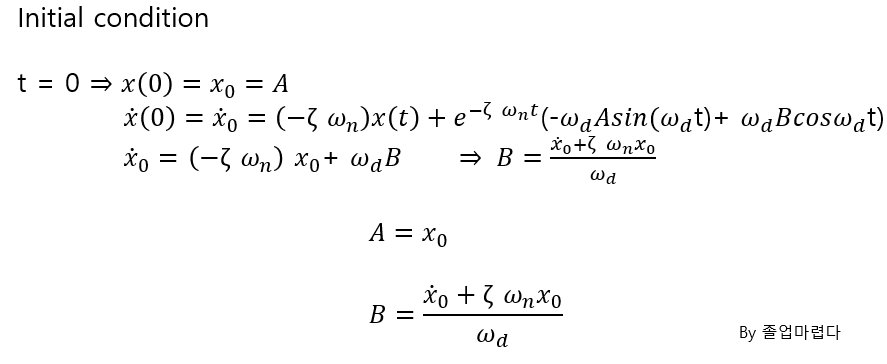
이제 particular solution을 구하면 됩니다.

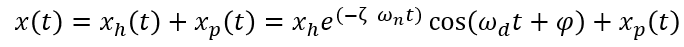
particular Solution

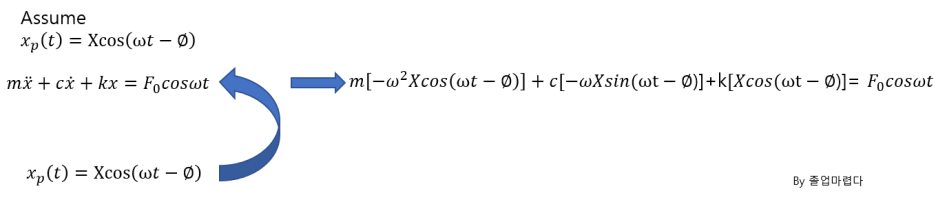
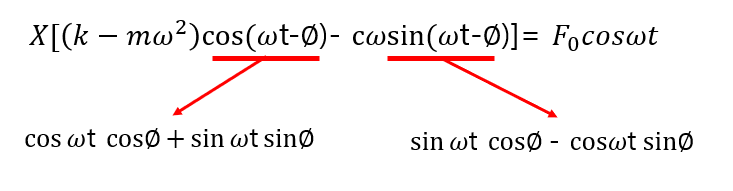
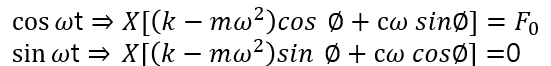
이를 Magnification factor 라고 합니다.

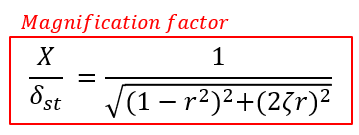
파이는 phase angle로 다음과 같이 표현됩니다.

위 식을 보면 비감쇠 자유진동에 댐핑계수 C가 추가되었으므로 이를 간단히 할 새로운 개념이 필요합니다.

이에 적용되는 새로운 개념이 감쇠비 Damping ratio입니다.

위 Damping ratio를 식에 적용하면 다음과 같은 결과가 나옵니다.

고유진동수 포스팅에서와 같이 결과를 예상하고 대입하였을 때 맞으면 되는 것으로 다음과 같이 예측하고 대입하게 됩니다.

이제 이렇게 구한 s를 원래식에 대입하면 다음과 같습니다.

마지막 줄에 euler fomula에 의해 다음과 같이 나오는데 Euler fomula는 다음과 같습니다.

Euler fomula

여기서, e는 자연로그의 밑인 상수이고, i는 제곱하여 -1 이 되는 sin cos 은 삼각함수의 사인과 코사인 함수입니다.

x에 pi를 대입하여,  e^(i*pi)+1=0 이라는 오일러 등식이 결과입니다.

위에서 구한 A와 B를 대입하면 다음과 같은 결과를 도출할 수 있습니다.

위에서 구한 식을 그래프로 그리면 다음과 같이 나오게 됩니다.

Damping ratio의 값에 따라 결과가 달라지는데 다음과 같은 경계로 나타낼 수 있습니다.

외팔보를 이용한 진동감쇠기 (Seismic Design)내진설계

모든 물체는 고유진동수를 가지고 있고 조화가진 시 가진주파수와 고유진동수가 일치하게 되면 공진이 발생하여 파괴되는 문제가 있습니다.

이러한 공진문제를 해결하는 방법중 하나로 공진주파수가 같은 물체를 부착하면 이론적으로 진폭이 0이되는데 이를 알아보도록 하겠습니다.

진폭이 0이 되는 공학적이유는 아래와 같습니다.

사진 설명을 입력하세요.

EX) 만약 11HZ의 고유진동수 (Natural frequency)를 가진 물체가 있을 때 이와 같은 진폭을 가진 물체를 만들어 보도록 하겠습니다.

아래와 같이 동전을 이용하여 외팔보형태의 기구를 설계하면 됩니다.

사진 설명을 입력하세요.

외팔보 형태로 만든 이유는 정확히 등가질량(Equivalent mass)을 계산할 수 있고(23.6% 이는 적분법으로 구하면 되는데 다음에 알아보도록하겠습니다.) 직접만들기 쉽기 때문입니다.

이렇게 얼추 비슷하게 만들고 ANSYS 를 통해 이론값이 맞는지 확인합니다.

ANSYS도 이론값이긴 합니다...

좌 : 1차 모드 우 :2차 모드

1차고유진동수는 11.053HZ로 왼쪽과 같은 Mode shape를 보이고 2차고유진동수는 148.34HZ로 Mode shape를 보면 트위스팅되는 것을 볼 수 있습니다.

이 결과를 잘 생각해보면 트위스팅되기 까지가 어렵다라는 결론과 실제 내진설계와 같은 공학설계에서는 높은차수까지 고려할 필요성이 없다는 것을 유추해 볼 수 있습니다.

이를 실제로 알아보기 위해 가속도 센서를 부착 후 실험한 결과는 다음과 같습니다.

실제 공진주파수 대역에서의 가속도 측정결과.

사진 설명을 입력하세요.

위의 결과에서 보듯 공진영역의 진폭이 0에 가깝게 된 것을 볼 수 있다.

댐핑없는 자유진동시스템에서의 고유진동수는 강성(K)와 질량(m)의 함수이다.

이러한 고유진동수를 가지고 있는 물체에 고유진동수와 같은 주파수의 가진이 주어지면 진폭이 중첩되어 진폭이 무한대가 되는데 이러한 현상을 공진(Resonance)라고 한다.

if wn(고유진동수) = w(가진주파수 -> 공진resonance