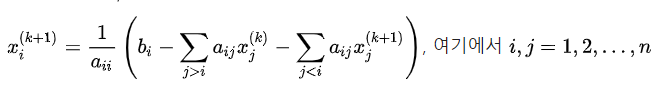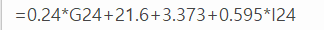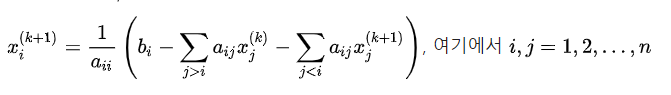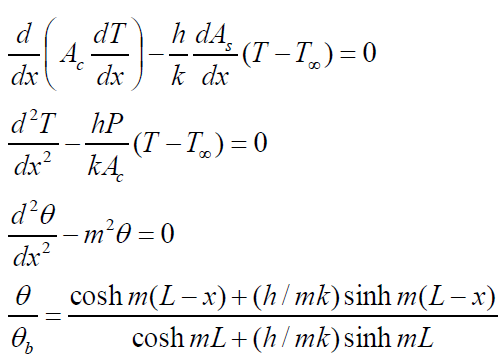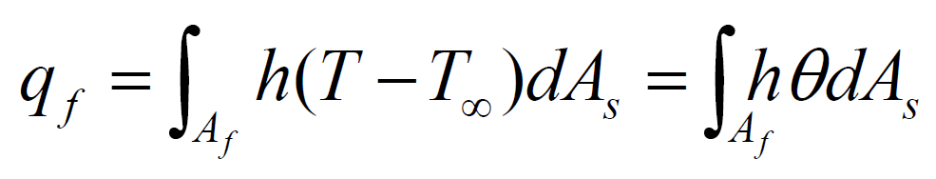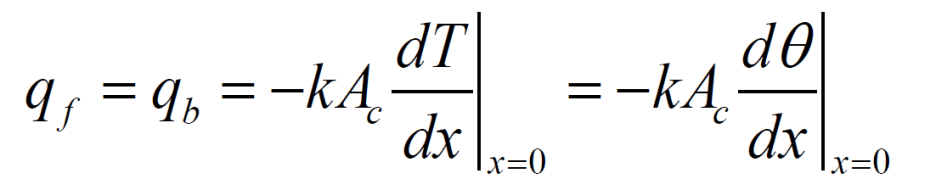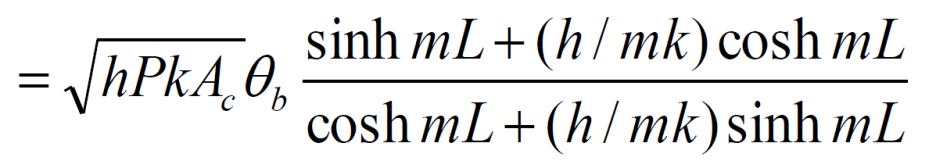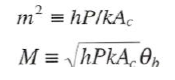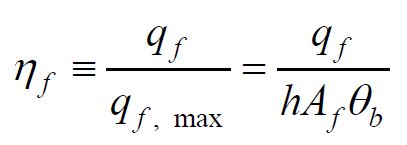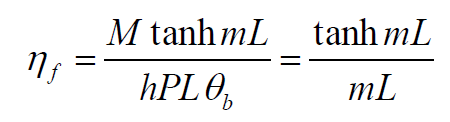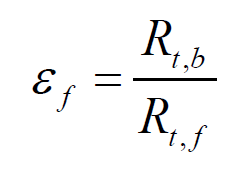몽키로 전력 변환하기

안녕하세요

이번에는 열전달에서 많이 사용되는 수치해법 중 하나인 Gauss seidel 에 대해 알아보도록 하겠습니다

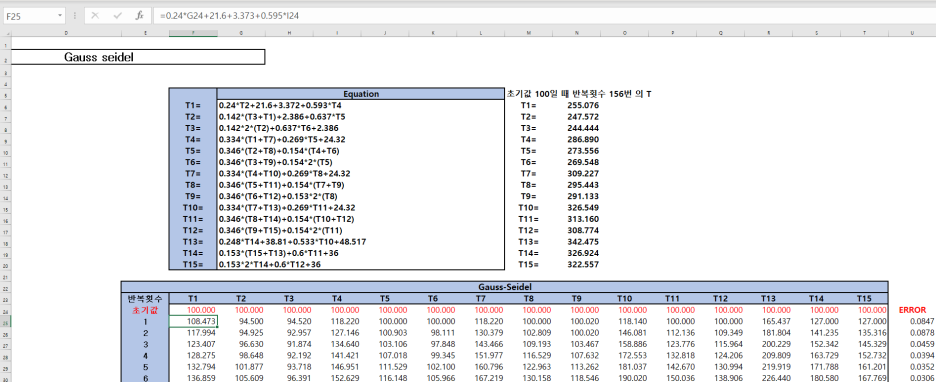
만약 아래와 같은 미지수가 15개인 15차 연립방정식이 있다면 손으로 푸는것은 가능은 하겠지만...

저는 절대 못합니다.

(4차만 되더라도 정신병걸릴거 같아서....)

이 때 사용하는 방식이 Gauss seidel 입니다.

matlab을 사용하신다면 inv(A)를 통해 이 방식보다 훨씬 쉽게 풀 수 있지만 matlab이 없다면

엑셀로 풀 수 있는 방식이 Gauss seidel입니다.

이론은 이전의 값을 현재식에 대입하여 다시 구하고 이 방식을 반복하여 이전값과 현재의 값의 차이가 설정해놓은

오차 이내에 들어오면 해로 판정하는 방법입니다.

이론은 아래와 같은데 간단한걸 어렵게 표현한 식입니다.

그냥 이전값(처음에는 초기값을 임의로 설정)을 방정식에 대입해서 나오면 나온값이 이전값이되고 다시 방정식에 대입 이런 걸 계속 반복하면 됩니다.

방법은 매우 간단합니다.

1. 위의 식에 맞게 이전의 셀을 식에 넣어주면 됩니다

2.이후 드래그를 통해 생성

3. Error는 보고싶은 값 (저는 T1을 기준으로 [Error=Abs(Tn+1-Tn)/Tn] 식을 만들었습니다)

이 식을 보시면 아시겠지만 이전의 값이 현재 값과 얼마나 다른가 비율로 나타내는 식입니다.

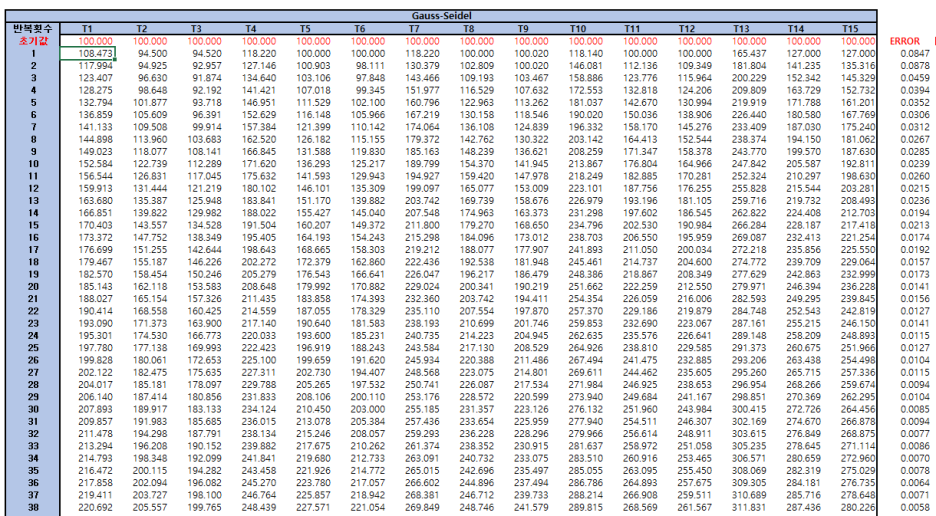
4.결과(저는 Error를 0.0001보다 작으면 표기되도록 조건부 서식에서 설정했습니다.

열전달 계산 Mathlab 프로그래밍(feat.Gauss seidel)

열전달 문제는 Gauss seidel 방식으로 해결할 수 있습니다.

전에 엑셀프로그램으로 계산방법을 포스팅했었는데 오늘은 매트랩(Mathlab)의 GUI기능을 이용하여 프로그램을 만들어 보도록하겠습니다.

먼저 Gauss seidel방식의 수식은 다음과 같습니다.

이 식의 의미는 이전의 값을 현재식에 대입하여 다시 구하고 이 방식을 반복하여 이전값과 현재의 값의 차이가 설정해놓은 오차 이내에 들어오면 해로 판정하는 방법입니다.

즉 이전값(처음에는 초기값을 임의로 설정)을 방정식에 대입해서 나오면 나온값이 이전값이되고 다시 방정식에 대입 이런 걸 계속 반복하면 됩니다.

이를 프로그래밍을 통해 구현하면 다음과 같습니다.

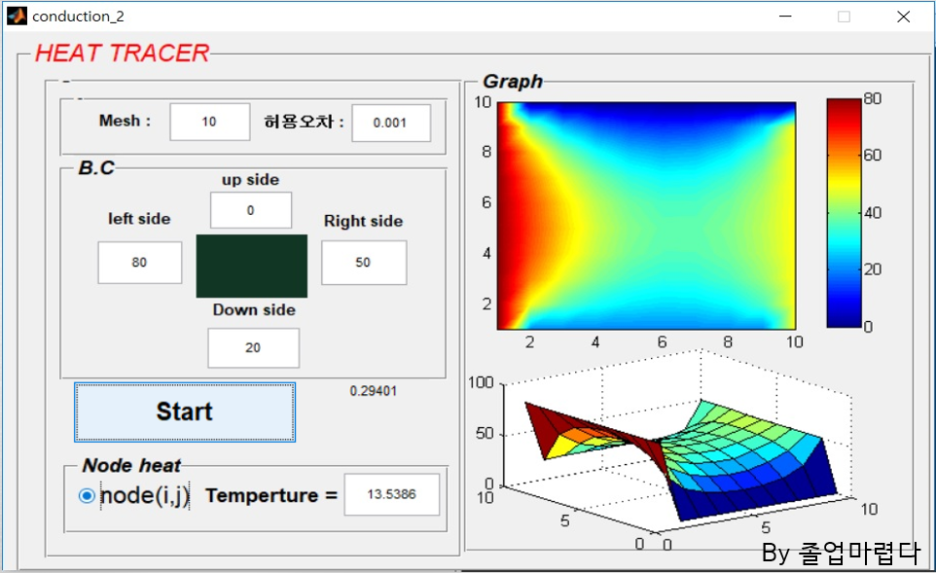
이를 GUI로 표현하면 다음과 같은 결과를 도출할 수 있습니다.

온도를 측정하는 방법중 하나인 열전대에 대해 알아보도록 하겠습니다.

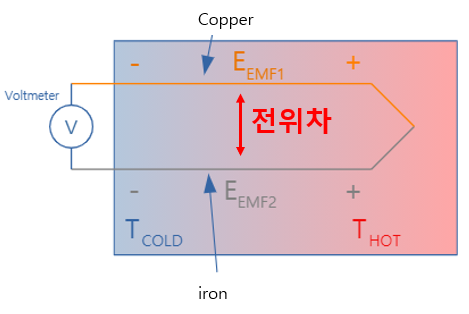
성분이 서로 다른 두 종류의 금속으로 폐회로를 만들어 양쪽의 온도를 달리해 주면 회로 내에 기전력이 발생하는 제백(Seebeck)효과를 이용하여 온도를 측정합니다. 즉, 기준온도와의 온도 차이에 의해 발생되는 기전력의 차이를 측정함으로써 온도를 알 수 있습니다.

열전대는 다음과 같은 물질로 이루어 집니다.

열전대의 장점은 비교적 짧은 지연 시간, 즉 온도 변화에 매우 빠르게 반응합니다. 또한 열전대는 기계적으로 매우 견고하며 유형에 따라 -250 ° C ~ +2000 ° C의 온도 범위를 측정할 수 있습니다. 또한 두 열전대와이어의 접촉점에서의 전위차를 측정하는 것 이기 때문에 점접촉만으로도 측정이 가능하기에 공간 절약형 설계로 인해 열전대는 접근하기 어려운 위치에 쉽게 도달 할 수 있습니다.

열전대는 중간 부분의 온도변화는 두 접점 사이의 기전력에 영향을 주지 않고

기준 금속에 대한 어떤 두 금속의 기전력이 각각 리스트화 되어있다면 그 두 금속으로 이루어진

회로의 기전력은 그들의 기준 금속에 대한 기전력의 차이와 같습니다.

이러한 기전력의 차이를 측정하는 장비는 요코가와 사의 MX100이 있습니다.

MX100은 데이터 로깅 요구 사항에 대해 4채널에서 1200채널까지 대응 가능합니다.

이러한 장비와 컴퓨터의 연결을 통해 정확한 온도값을 찾을 수 있습니다.

앞선 포스팅에서 알아본 전도와 대류를 통해 fin의 온도분포 열전달율 효율등을 구할 수 있습니다.

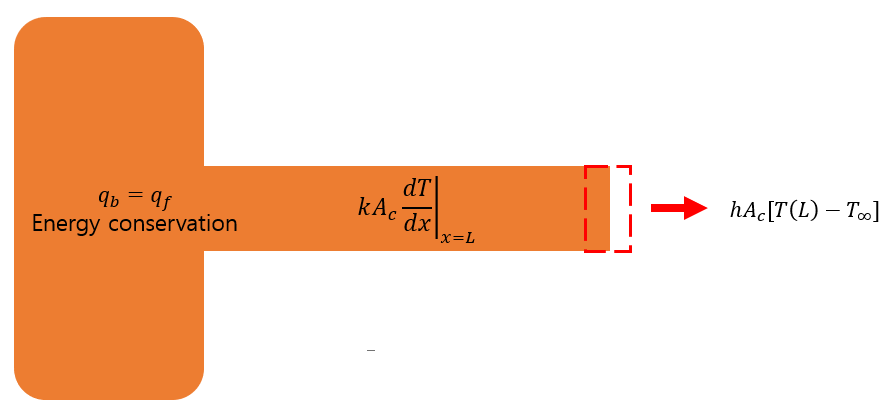
아래의 그림은 열전도로 들어온 열은 Energy conservation에 의해 대류로 모두 빠져나간다는 것을 바탕으로

식이 유도된 것입니다.

아래의 그림은fin끝이 대류열전달상태일때를 나타냅니다.

특정위치에서의 핀의 온도의 비는 아래와 같이 유도됩니다.

열전도와 대류열전달로인한 열전달율이 같다는 가정에 의해 다음과 같은 din의 열전달율은 다음과 같습니다.

위와 같은 방법으로 Fin끝이 단열 특정온도 무한fin일때를 유도해 보면 다음과 같은 표로 나타낼 수 있습니다.

다음으로는 Fin의 효율에 대해 알아보도록 하겠습니다.

fin 효율은 다음과 같이 정의 됩니다 즉 fin을 통한 최대 열전도율에 대한 fin을 통한 실제 열전도율의 비입니다.

위의 식에 표에있는 수식을 대입하면 Fin끝 단열시에는 다음과 같은 식이 도출됩니다.

Fin효율을 구할 때 핀끝이 단열되어 있다고 가정하에 푸는 경우가 많기 때문에 이정도의 핀끝단열효율은 외워두는 것이 좋습니다.

다음으로는 Fin의 유효도입니다.

fin 유효도는 다음과 같이 정의 됩니다 즉 fin이 없을 때 열전도율에 대한 fin이 있을 때 열전도율의 비입니다.

Fin과 base의 온도는 steady state이므로 같은 온도를 가진다는 가정이므로 저항으로만으로도 유효도를 아래와 같이 구할 수 있습니다.

유효도 식을보면 fin의 대류저항이 커질수록 유효도는 떨어진다는 것을 유추할 수 있습니다.

이를 통해 만약 한쪽면이 물 다른 한쪽이 공기와 맞닺아 있는 상황이라면 대류열전달계수가 낮은 공기와 맞닫는 면에 Fin을 설치해야 한다는 것을 알 수 있습니다.

그래서 Fin은 수냉보다는 대부분 공냉시에 사용됨을 알 수 있습니다.

지금까지 Fin의 설계에 대해 알아보았습니다.

다음포스팅에서는 ansys CFD를 통한 강제대류 및 자연대류에 대한 해석을 진행해 보도록 하겠습니다.