반응형

오늘은 유체역학에서 중요한 방정식중 하나인 베르누이방정식에 대해 알아보도록 하겠습니다
베르누이방정식은 유선상에서의 정압과 동압의 합은 항상 일정하다라는 식입니다
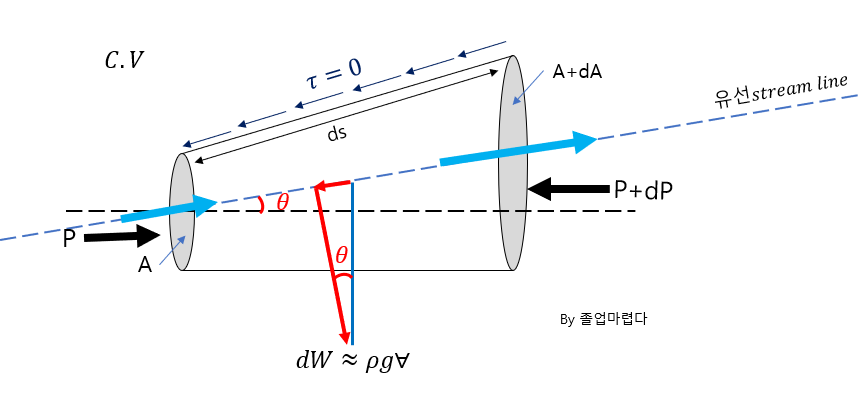
아래와 같이 C.V을 잡고 아래 두개의 가정하에 적용이 됩니다.
1.frictionless flow (즉 마찰은0)
2.along streamline in frictionless flow
먼저 Reynolds Transport thorem (레이놀즈 수송정리)를 바탕으로
mass conservation과 momentum conservation을 정의하게 됩니다
레이놀즈수송정리에 관한 유도과정은 레이놀즈수송정리 포스팅을 참조하시기 바랍니다

1. mass conservation의 적용 ( B=1, β =1)

2. The linear momentum conservation(B=mv, β =v)
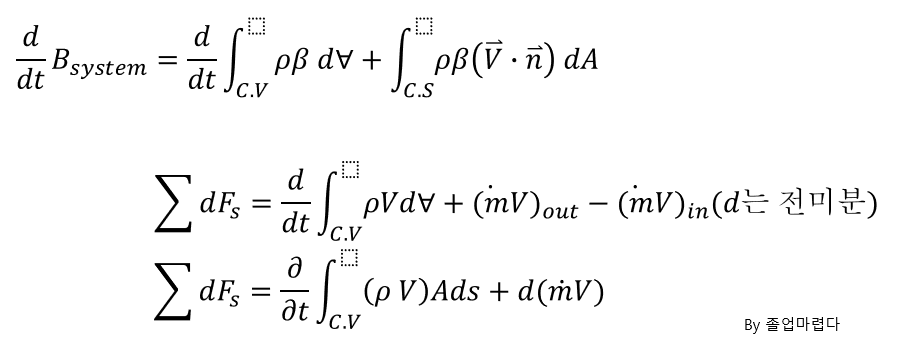
여기서 differential이 round로 변한이유는 아직 steady state인지 incompressive인지 결정되지 않아 round로
쓴 것으로 시간에 따라 변할 수 있는 상태입니다.
유체역학에서 유체에 작용하는 힘 F는 3가지가 있습니다
1.gravity(중력)
2. pressure
3.shear force (frictionless flow라 가정하였기 때문)
이러한 힘들을 위의 식에 대입하면 다음과 같이 도출됩니다

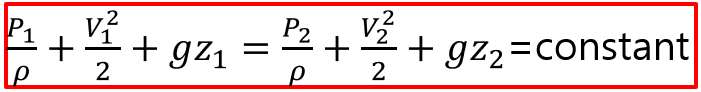
반응형
'기계공학(Mechanical Engineering) > 유체역학(Fluid Mecahnics)' 카테고리의 다른 글
| 관 마찰계수 (수두손실) 유도 (0) | 2022.10.21 |
|---|---|
| 파이프유동 pipe flow (couette flow and poiseuill flow by viscous and pressure) (0) | 2022.10.21 |
| 수평pipe에서의 층류유동hagen poiseuille's law의 유도 Navier-stokes and C.V sol (0) | 2022.10.21 |
| 경계층이론 boundary layer(feat 블라시우스상사,폰카르만 적분방정식) (0) | 2022.10.21 |
| 골프공이 멀리나가는 이유(딤플) (0) | 2022.10.21 |