몽키로 전력 변환하기

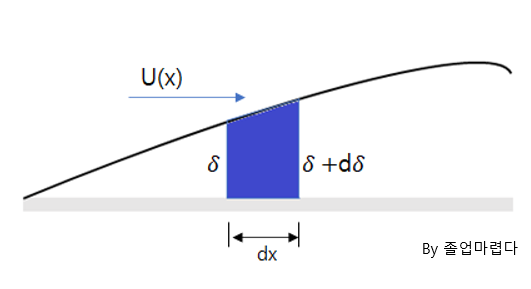
유체가 흐르다 수평의 평판과 만나게 되면 평판의 점성에의한 마찰로 흐르던 속도가 줄게되고 이에따라 다음과 같은 속도 profile을 갖게 됩니다.

여기서 점성의 영향을 받는 viscous layer인 boundary layer와 점성의 영향을 받지 않는 booundary layer 밖의 영역으로 나뉘게 됩니다.

 

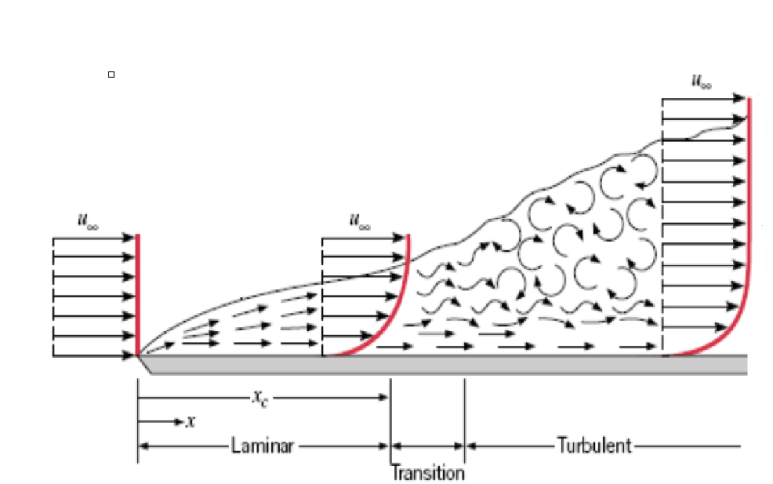
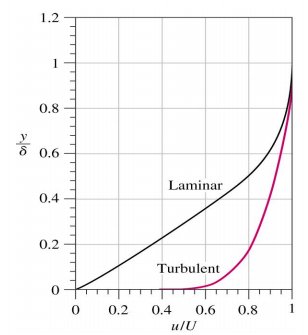
figure (1) 좌 boundary layer 우 velocity profile

여기서 viscous의 영향을 받는 경계층 두께의 기준은 원래유동속도 U_inf의 99%(책마다 조금씩 다릅니다)가

되는 지점으로 정의합니다.

유체역학에서는 유체의 거동(위치 속도 압력)을 알기가 어려운점이 있기때문에 대부분의 식들은 실험을 통해 나온결과가 많습니다.

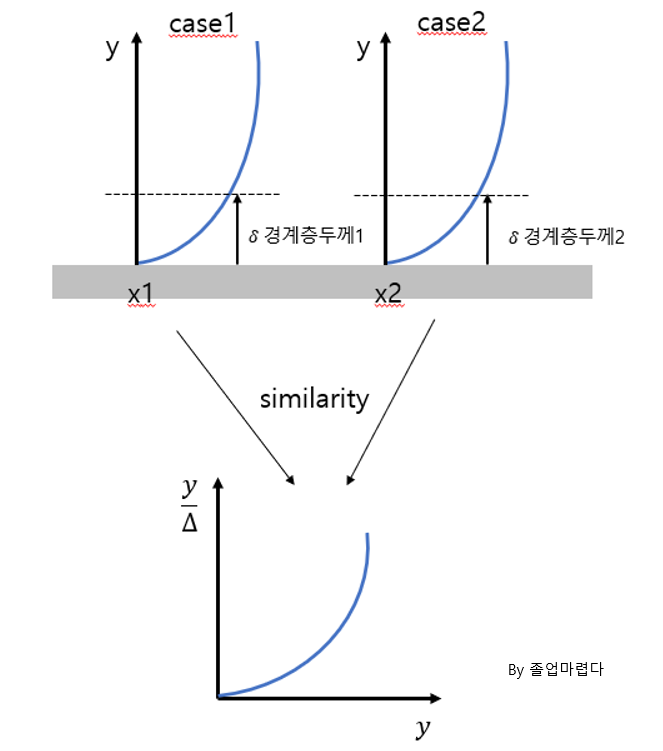
실험에 사용되는 모형 이외에도 같은식을 사용하기 위해 무차원화 된 단위를 사용합니다.

아래의 그림을 보면 boundary layer에서 속도는 x에따라 변하게 되는데 물리량을 무차원화 하면 하나의 그래프로

오늘은 여러가정하에 유도하여 적용할 수있는 B.L에 적용되는 식에대해 알아보도록 하겠습니다

표현이 가능하다는 것을 표현한 그림입니다.

이때 속도u 는 아래(1) 와 같이표현이 가능하다 가정하고 이를 Similarity solution이라고 합니다.

블라시우스상사

 

이렇게 가정하였을 때 continuity equation(질량보존)과 Navier-Stokes Equation운동량보존을 만족하면

무차원화한 것이 유효하다고 볼 수 있습니다.

이러한 무차원화에 대한 증명을 하기 전에 B.L(Boundary layer)에 대한 명칭과 의미에대해 알아보도록 하겠습니다.

 

이러한 블라시우스 상사가 성립되면 좋은점은

유체가 받는 stress와 음직임은 속도 V와 pressure만 알면 Navier-stokes, continuity equation을 사용하지 않고도 유체의 거동을 알 수 있다는 점입니다.

 

경계층이론

 

 

위의 3개의 boundary layer에서의 명칭에대한 의미와 유도를 하기전에 폰카르마적분방정식 먼저 알아보도록 하겠습니다.

 

 

 

폰카르만 적분방정식

 

C.V을 잡고 폰카르만 적분방정식을 통해 층류와 난류 모두의 속도분표를 알 수 있는데 만약 속도분포를 안다면

연속방정식(질량보존)과 운동량보존(나비에스토크스)를 통해 경계층두께 벽전단력 그리고 항력을 구할 수 있습니다.

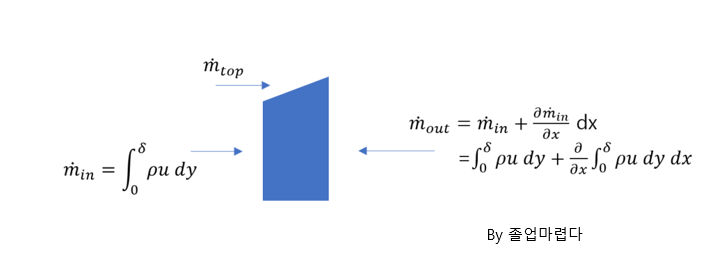
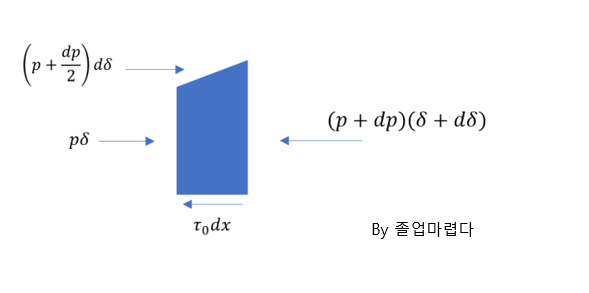
먼저 폰카르만 적분방정식에 대해 유도하면

 

 

(1)Mass flux

 

 

(2) Forces

 

 

 

(3) momentum flux

 

 

 

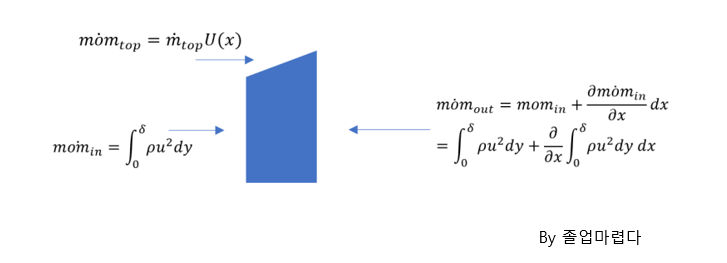
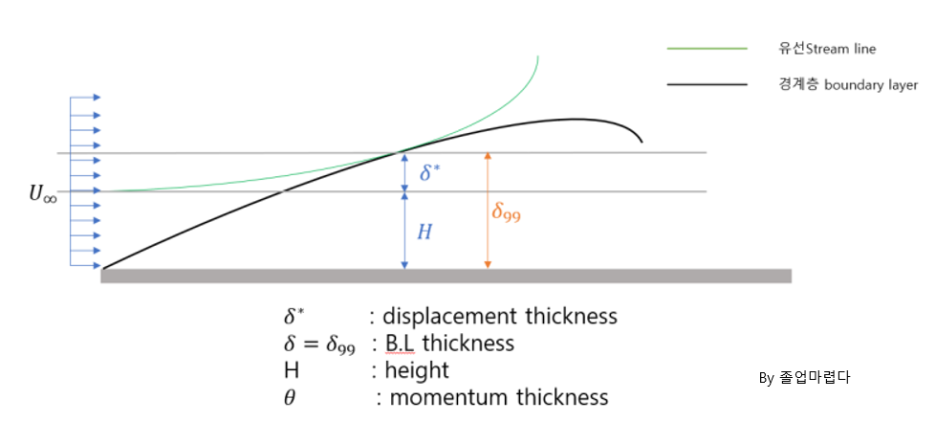
1.boundary layer thickness

 

boundary layer는 경계층두께로 정의되고 초기유동속도의 99%의 위치까지의 높이를 의미합니다

이러한 경계층두께는 난류가 층류에 비해 빠르게 U_99에 접근하는 것을 볼 수 있습니다

그렇기 때문에 난류가 층류에 비해 경계층 두께가 얇은 특징이 있습니다.

 

2.displacement thickness

위의 폰카르만 적분방정식에서 (1) mass flux를 보면

U_inf*H의 체적유량으로 들어오던 초기유량이 평판의 점성에 의해서 속도가 줄게되고 이에 따라

질량보존을 만족하기 위해 증가한 경계층두께를 나타내는 것 입니다.

 

 

 

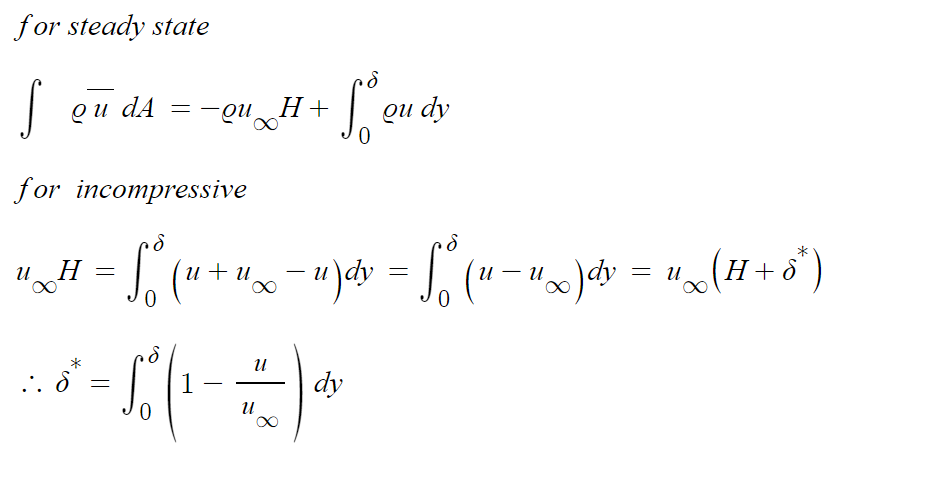
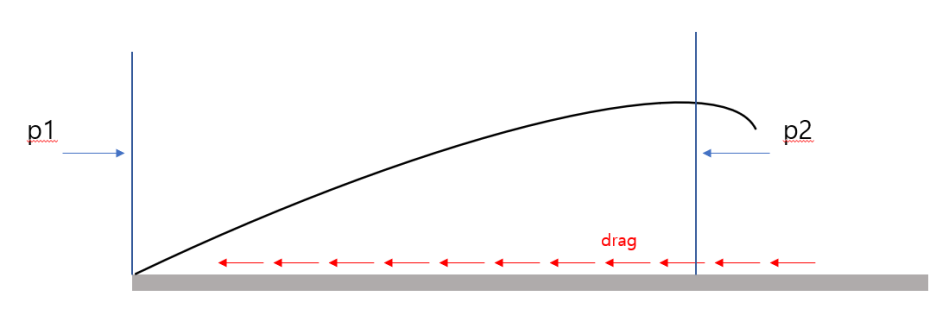
3. momentum thickness

momentum이 평판의 수직으로 확산되면서 확장되는 두께를 나타내고 운동량감소를 나타냅니다.

 

 

drag는 마찰에의한 항력으로 아래와 같습니다.

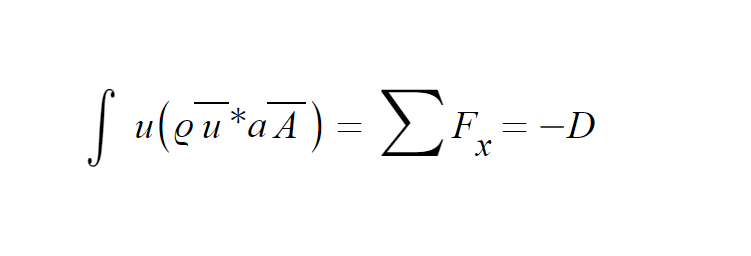
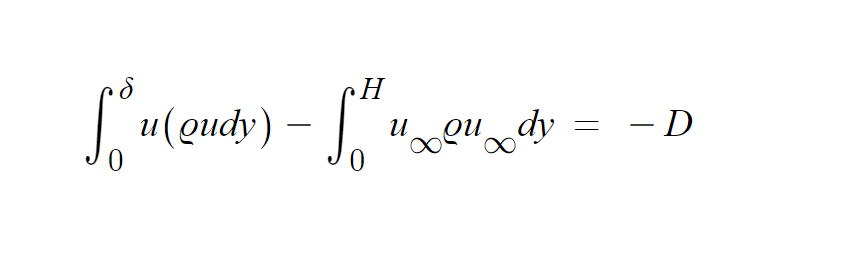
since

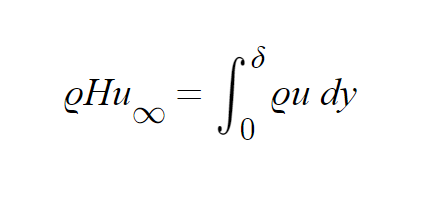
위와 같은 조건에 의해 다음과 같이 drag가 도출됩니다.

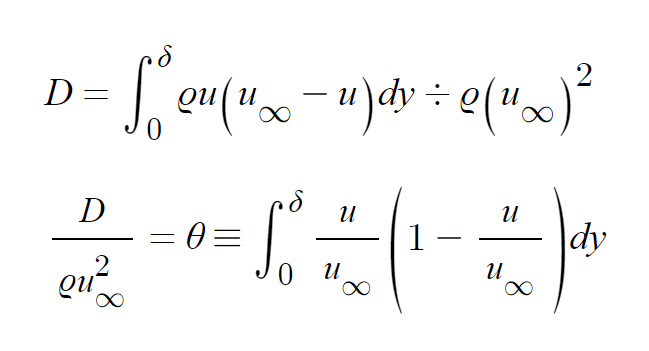
결론적으로 momnetum감소에 따른 Drag는 다음과 같이 도출됩니다.

 

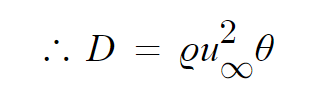
지금까지 점성에 의해 발생하는 Boundary layer상에

displacement thickness ,momentum thickness 과 이로인한 Drag force의 유도과정에 대해 알아보았습니다.

 

골프공을 자세히 보신적이 있나요?

골프공을 보면 움푹파인 홈들이 있는데 이를 딤플이라고 합니다.

이러한 딤플에 의해 골프공이 멀리 나가게 되는데,

오늘은 왜 골프공이 딤플에 의해 멀리나아가게 되는지 유체역학의 원리를 적용하여 설명하도록 하겠습니다.

결론먼저 쓰면

- 딤플은 유체의 흐름을 난류로 만든다.

- 난류에 의해 박리점이 공 뒤로 간다.

- 이로인해 형상항력을 줄일 수 있다.

이러한 결론을 내기 위해 몇가지 유체역학의 이론에 대해 설명하면

먼저 유체의 흐름에는 층류와 난류가 있습니다

층류는 층층히 나뉘어져가서 층류고, 난류는 규칙없이 난잡하게 유동합니다.

이러한 층류와 난류를 정의하는 무차원의 수를 레이놀즈수(Reynolds number)라고 합니다

각각의 레이놀즈수는

층류 Re < 2300

난류 Re > 4000

입니다

층류와 난류형태로 흐르는 유체가 고체를 만나면 고체의 벽면을 따라 경계층(boundary layer)을 형성하고

점성효과(viscous)를 받는 경계층 내부구역과 점성효과를 안받는 경계층 외부구역(inviscous)으로 나뉩니다

이러한 경계층의 기준은 초기유동속도의 99프로가 되는 곳으로 아래 유동프로파일(유동속도)그래프를 보면 난류가 층류보다 가파르게 속도가 증가함을 볼 수 있습니다

즉 표면에서 수직방향으로 올라갈 때 난류가

초기 유동속도의 99프로에 더 빠르게 근접하므로 경계층 영역의 길이가 짧게 형성됩니다.

경계층의 두께의 경우는 난류가 층류이후에 발생함으로 난류가 더 두껍게 나타납니다.

경계층 두께 는

층류 < 난류 가 됨을 알 수 있습니다.

경계층의 영향을 받는 길이는

층류>난류

다음으로 알아야 할 이론은 박리입니다.

박리란 유체가 고체면을 만났을 때 점성효과로 인해 속도가 줄어 고체의 속도를 따라가지 못해 떨어져 나가는 현상입니다.

박리의 특징은 순압력구배(dp/dx < 0) 에서 역압력구배(dp/dx > 0)로 넘어가는 지점으로 가장 압력이 낮은 지점입니다.

위 사진과 같이 난류일경우 박리점이 뒤에 있음을 볼 수 있습니다.

난류이면 왜 박리점이 뒤로 가는가?

여기서 Re 수와 C_D의 관계를 나타낸 그래프가 아래에 있습니다.

위 그래프를 보면

난류가 층류보다 C_D값이 낮기 때문에 Drag force를 적게 받는다는 것을 알 수 있습니다.

정리하면

경계층의 길이 층류 >난류 로 난류가 viscous영향을 적게 받고 C_D 값이 낮기 때문에 난류의 박리가늦게 발생합니다 .

이러한 낮은압력의 박리점이 뒤로감으로서 압력차에 의한 형상항력을 받는 공의 면적이 줄어 더 멀리 나갈 수 있는 것 입니다.

결론

- 딤플은 유체의 흐름을 난류로 만든다.

- 난류에 의해 박리점이 공 뒤로 간다.

- 이로인해 형상항력을 줄일 수 있다.

이로인해 딤플이 있는 골프공이 멀리나가게 됩니다