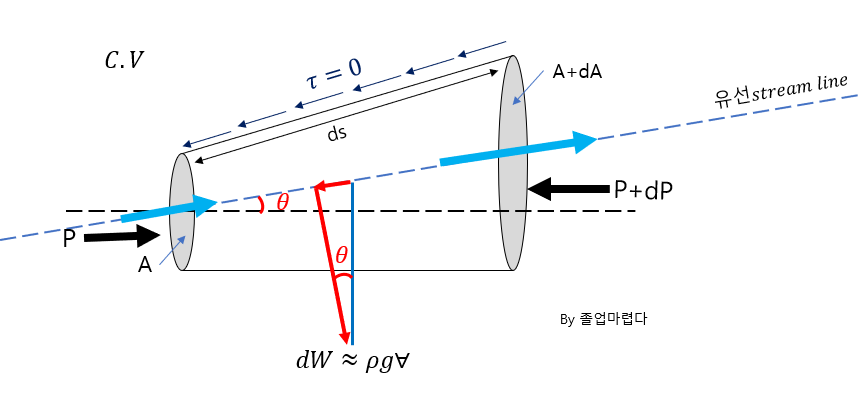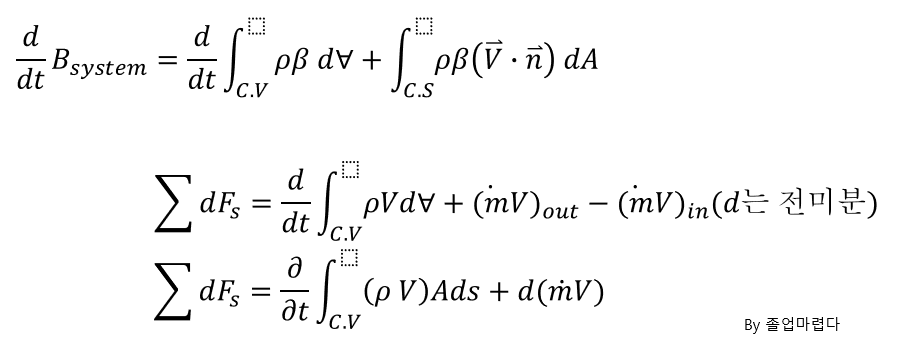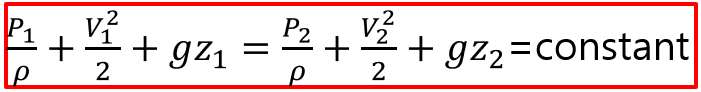
다음과 같은 상태일 때 다음과 같은 C.V을 잡고 force를 계산하면 전단력이 다음과 같이 유도 됩니다.

이후 뉴턴유체이고 베르누이방정식을 적용시키면 다음과 같이 유도됩니다.
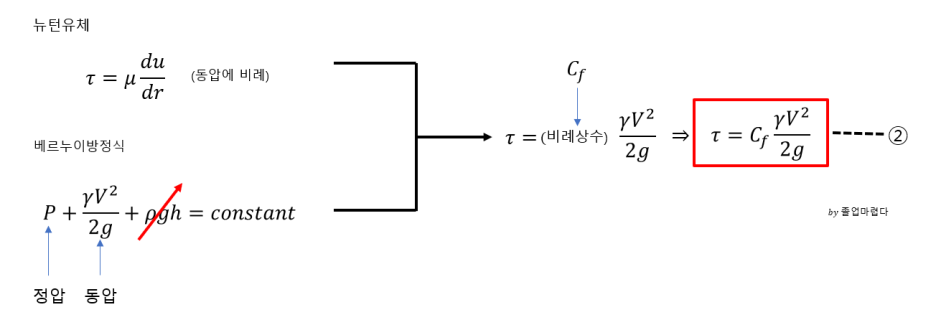
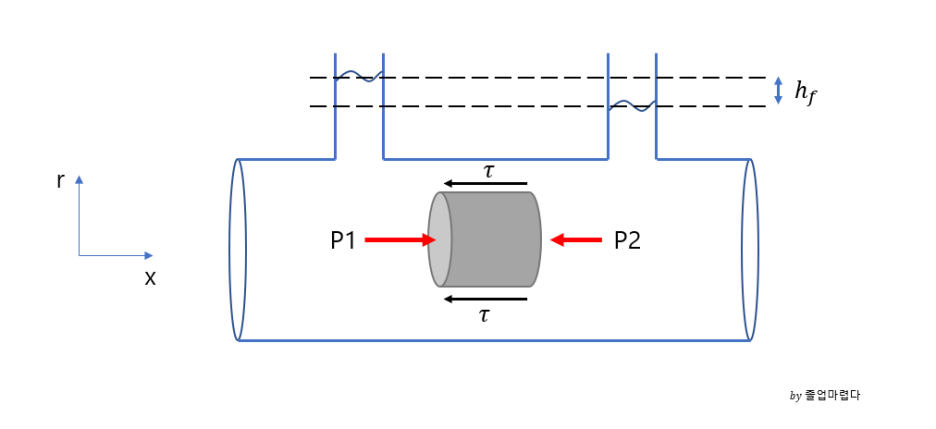
위에서 나온 1번식과 2번식을 같다고 놓고 풀면 압력차는 최종적으로 다음과 같이 나옵니다.

위에 h_f가 수두손실입니다.
'기계공학(Mechanical Engineering) > 유체역학(Fluid Mecahnics)' 카테고리의 다른 글
| 연속방정식 continuity equation(mass conservation) (0) | 2022.10.21 |
|---|---|
| 유체역학 입자유동 회전 와도 순환(rotation,vorticity,circulation) (0) | 2022.10.21 |
| 파이프유동 pipe flow (couette flow and poiseuill flow by viscous and pressure) (0) | 2022.10.21 |
| 수평pipe에서의 층류유동hagen poiseuille's law의 유도 Navier-stokes and C.V sol (0) | 2022.10.21 |
| Bernuii Equation 유도(베르누이방정식) (0) | 2022.10.21 |