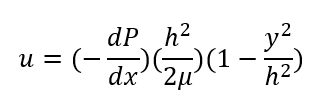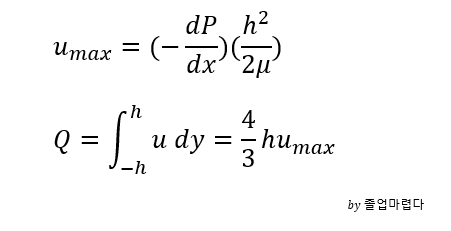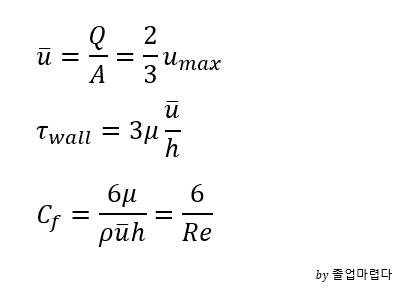앞선 포스팅에서 laplace equation을 만족하면 potential flow를 만족한다고 알았습니다.
이를 통해 velocity potenti
al을 다음과 같이 정의할 수 있습니다.
이번에는 invicid 상에 유동장을 설명하기위한 추가적인 개념인 stream function에 대해 알아보도록 하겠습니다.
stream function은 다음과 같이 정의되고 크사이라고 읽으며 항상 continuity equation(mass conservation)을 만족하도록 되어있습니다.

만약 stream function이 일정한 경우를 생각해보면 다음과 같이 표현됩니다.
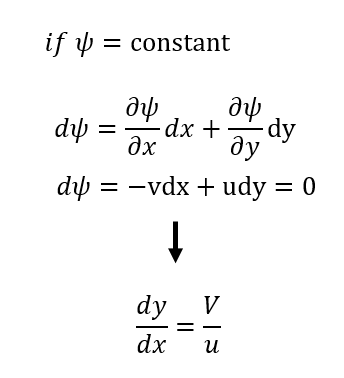
위의 최종식을 보면 stream line(유선)의 식과 같은 것을 확인할 수 있습니다.
이것을 통해 stream function이 일정하다면 유선과 같고 이름에 왜 stream이 붙었는지를 알 수 있습니다.
streamline에 관한 내용은 streamline 포스팅 참조
stream function이 일정하다면 일정한 stream line사이의 유량을 구해보면 다음과 같습니다.
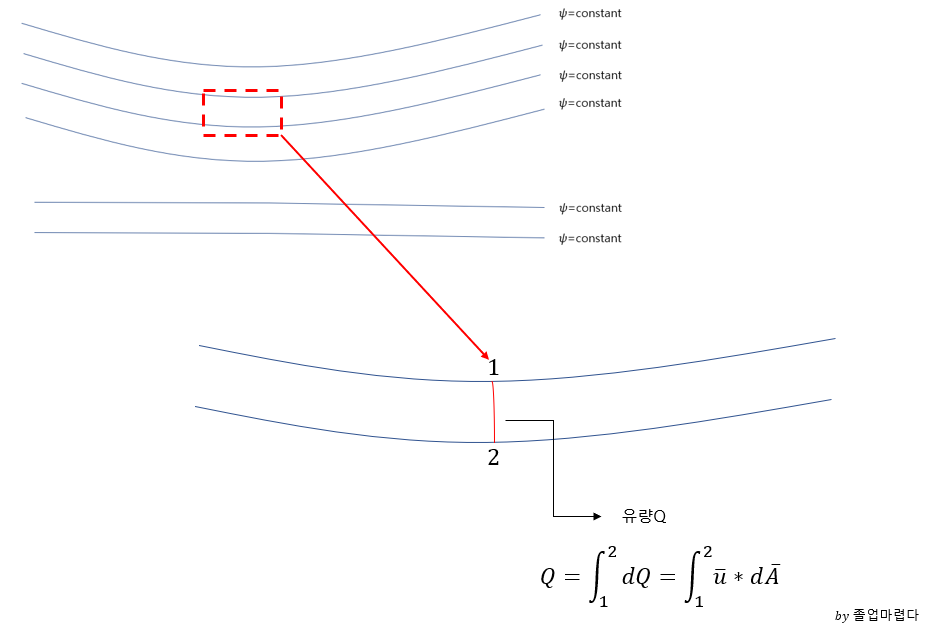
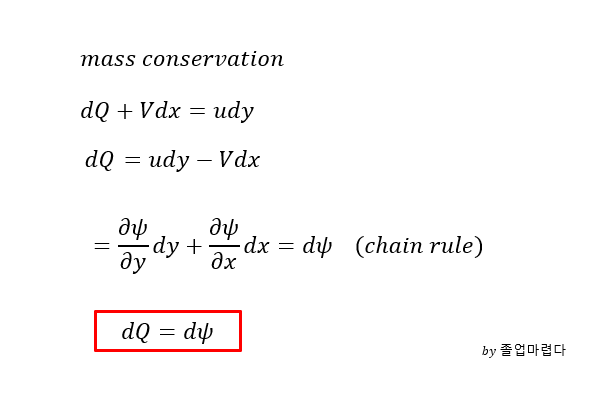
즉 일정한 stream function을 안다면 streamline의 차를 통해 유량의 변화를 알 수있습니다.
다음으로는 irrotational flow에서의 vorticity에 대해 알아보도록 하겠습니다.

즉 stream function이 irrotational flow이라면 laplace equation을 만족하여
앞선포스팅에서 확인했듯이 continuity equation을 만족하기 때문에 물리적으로 타당하다 할 수 있습니다.
다음으로는 velocity potential과 stream function의 관계에 대해 알아보도록 하겠습니다.

위와 같은 결과를 그림으로 표현하면 아래와 같습니다.
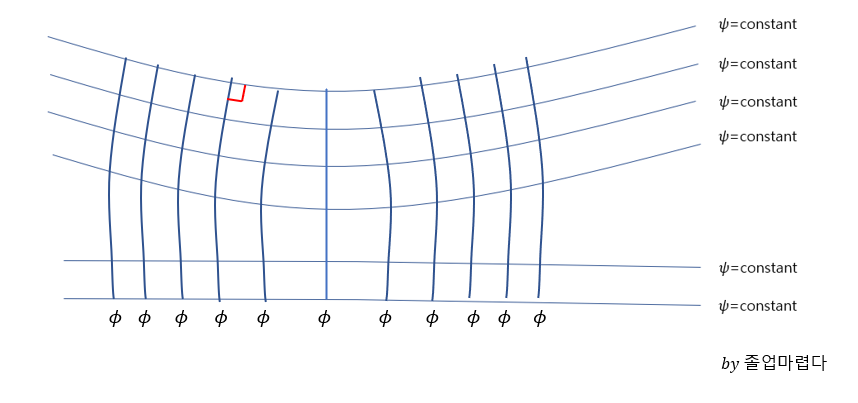
laplace equation을 통해 velocity potential을 얻고 위와 같은 velocity potential과 streamline(constant stream function)의 관계를 통해 flow pattern을 알 수 있습니다.
쉽게 말하면
속도
potential flow에서 laplace equation을 취하고 gradient로 속도를 구할 수 있습니다.
압력
베르누이방정식을 통해 pressure을 구한다.
(베르누이방정식은 streamline상에서만 유효합니다)
(베르누이방정식 포스팅 참조)
즉 Potential flow을 이용하면 비선형인 Euler equation을 풀지 않고서도 속도와 압력을 알 수 있습니다.
'기계공학(Mechanical Engineering) > 유체역학(Fluid Mecahnics)' 카테고리의 다른 글
| 유선,유적선,유맥선의 정의 (pathline, streakline,streamline) (0) | 2022.10.23 |
|---|---|
| Potential flow(#1 velocity potential )in invicid incompressive flow (0) | 2022.10.23 |
| Euler's equation(momentum conservation in invicid flow) (0) | 2022.10.21 |
| 연속방정식 continuity equation(mass conservation) (0) | 2022.10.21 |
| 유체역학 입자유동 회전 와도 순환(rotation,vorticity,circulation) (0) | 2022.10.21 |