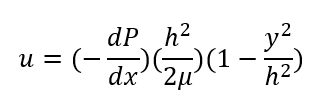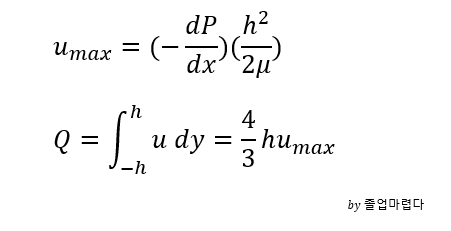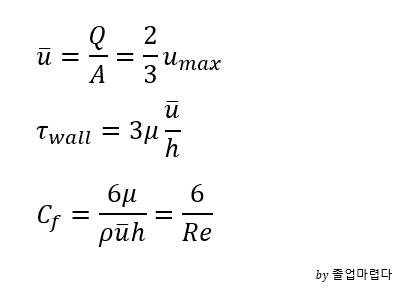유체역학에서 C.V내에서의 3가지 보존법칙(mass momentum energy)을 나타내는 equation은 3가지가 있고 다음과 같습니다.

그 중 유체역학의 꽃이라고도 하는 Navier-stokes equation에 대해 알아보도록 하겠습니다.
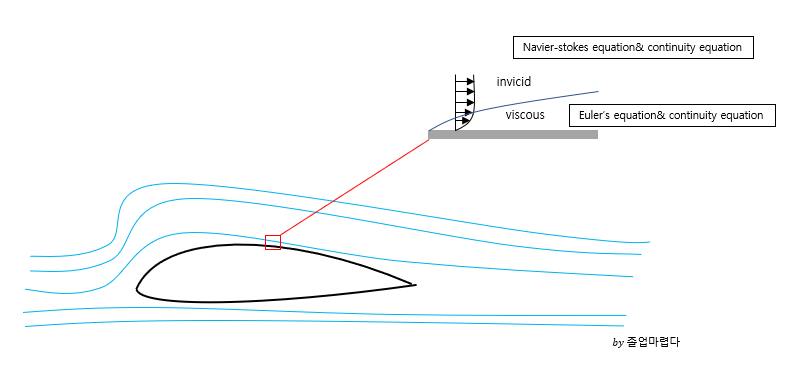
Navier-stokes equation은 invicid flow인 Euler equation에 viscous force를 추가하면 완성되는 식입니다.

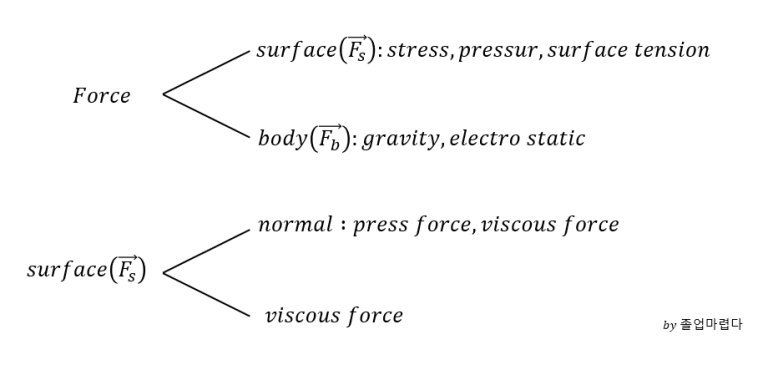
유체에 작용하는 force는 표면력(surface force)와 체적력(body force)가 있는데
viscous force는 표면력으로 다음과 같은 C.V에서 다음과 같이 유도될 수 있습니다.
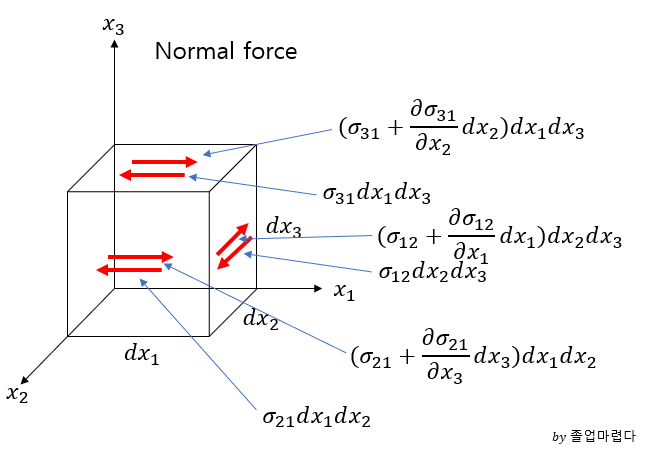
C.V에 작용하는 force를 index로 표현하면 다음과 같습니다.
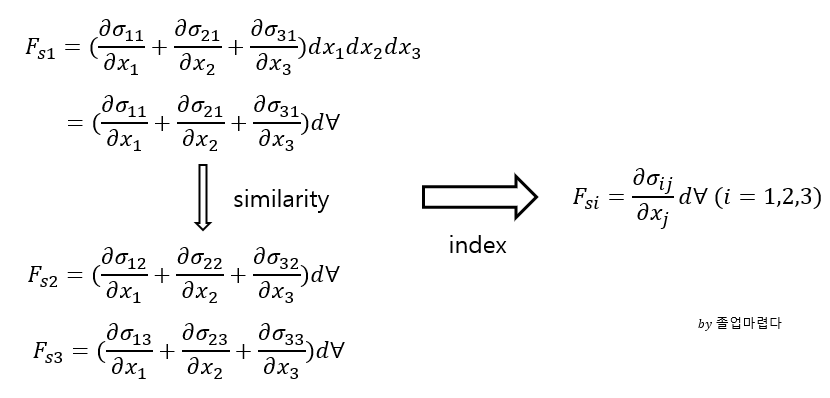
F_si 에서 나타내는 시그마는 pressure force와 viscous force의 합인 총 surface force로 다음과 같이 표현됩니다. 그리고 델타ij는 단위부피로 상수이기 때문에 미분시 소거되고 마지막으로 continuity equation에 의해
Navier-stokes equation은 다음과 같이 도출됩니다.

위의 Navier-stokes equation은 Newton-fluid 즉 점성계수가 constant하고 incompressive 즉 밀도가 일정할 때 viscous영역에서 사용할 수 있습니다.
다음 포스팅에서는 invicid region에서 이러한 복잡한 식을 이용하지 않고 속도와 압력을 구할 수 있는 potential flow에 대해 알아보도록 하겠습니다.